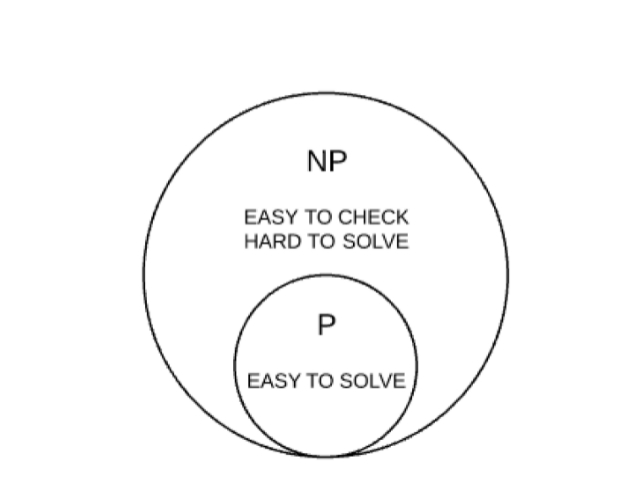
Η υπόθεση αυτή παραμένει άλυτη εδώ και 30 χρόνια. Το πρόβλημα αυτού του τύπου, «Ρ versus ΝΡ» -όπως λέγεται- εμφανίστηκε τη δεκαετία του 1970, όταν το διατύπωσαν οι Stephen Cook και Leonid Levin . Σύμφωνα με αυτή την υπόθεση, το Ρ σημαίνει εύκολο να βρεθεί λύση και το ΝΡ σημαίνει εύκολο να ελεγχθεί.
Η υπόθεση αυτή έχει να κάνει με το αν όντως υπάρχουν προβλήματα τα οποία είναι εύκολο να ελεγχθούν αλλά πρακτικά αδύνατο να λυθούν με άμεσες αλγοριθμικές διαδικασίες. Για παράδειγμα: Ας υποθέσουμε ότι πρόκειται να γίνει ένα εορταστικό τραπέζι και στα χέρια μας έχουμε 2 λίστες. Μια λίστα με 500 πιθανούς καλεσμένους και μια άλλη με ζεύγη αυτών των ανθρώπων που δεν πρέπει να εμφανιστούν στον τελικό κατάλογο των καλεσμένων. Είναι εύκολο να ελέγξουμε αν μια συγκεκριμένη λίστα 100 ατόμων, από 500 πιθανούς καλεσμένους, ικανοποιεί το κριτήριό μας να μην υπάρχουν ασύμβατα μεταξύ τους ζευγάρια στο τραπέζι. Το να δημιουργήσουμε όμως εμείς μια τέτοια λίστα από τους 500 πιθανούς καλεσμένους είναι τόσο δύσκολο που μοιάζει να είναι πρακτικά αδύνατο. Μάλιστα, ο αριθμός των εναλλακτικών τρόπων που μπορούμε να διαλέξουμε 100 καλεσμένους από τους 500 είναι μεγαλύτερος από το σύνολο των ατόμων που υπάρχουν στο σύμπαν, γι’ αυτό και στη λύση αυτού του προβλήματος δεν θα μπορούσε να βοηθήσει ούτε ο ισχυρότερος υπολογιστής.
Για προβλήματα όπως το παραπάνω, κανείς μέχρι σήμερα δεν έχει καταφέρει να δείξει ότι η λύση τους δεν είναι εφικτή με κατάλληλη προγραμματιστική μέθοδο.