Home » Άρθρα (Page 5)
Category Archives: Άρθρα
Όσα πρέπει να γνωρίζεις για τον Γιόχαν Καρλ Φρίντριχ Γκάους
Ο Γιόχαν Καρλ Φρίντριχ Γκάους, ο οποίος έμεινε γνωστός ως ο «Πρίγκιπας των Μαθηματικών», ήταν ένα παιδί-θαύμα, καθώς έκανε την πρώτη του σημαντική ανακάλυψη στην εφηβεία του. Έγραψε το περίφημο “Disquisitiones Arithmeticae”, το σπουδαιότερο έργο του, σε ηλικία μόλις 21 ετών.
Οι περισσότεροι γνωρίζουν τον Γιόχαν Καρλ Φρίντριχ Γκάους για την εξαιρετική ψυχική του ικανότητα. Αναφέρεται μάλιστα, ότι είχε προσθέσει τους αριθμούς από το 1 έως το 100, μέσα σε μόλις λίγα δευτερόλεπτα, ενώ βρισκόταν ακόμη στο δημοτικό σχολείο, με τη βοήθεια ενός έξυπνου τεχνάσματος
Ο Γερμανός μαθηματικός Γιόχαν Καρλ Φρίντριχ Γκάους συνεισέφερε σε πολλά ερευνητικά πεδία της επιστήμης του, όπως η Θεωρία Αριθμών, η Στατιστική, η Μαθηματική Ανάλυση, η Διαφορική Γεωμετρία, αλλά και συναφών επιστημών, όπως η Γεωδαισία, η Αστρονομία και η Φυσική. Ο ίδιος θέλησε να αποδείξει το θεμελιώδες θεώρημα της Άλγεβρας, και εισήγαγε την “Gaussian” βαρυτική σταθερά στη φυσική, καθώς και πολλά άλλα πριν καν γίνει 24 ετών!
Τέλος, ο Γιόχαν Καρλ Φρίντριχ Γκάους συνέχισε το σπουδαίο έργο του μέχρι τον θάνατό του, σε ηλικία 77 χρόνων, συμβάλλοντας δυναμικά στην πρόοδο και την εξέλιξη της επιστήμης του.
Ο δεύτερος θερμοδυναμικός νόμος
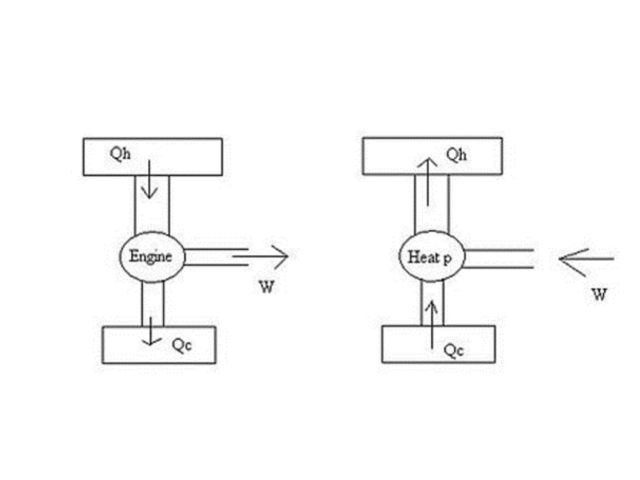
Ο δεύτερος θερμοδυναμικός νόμος είναι ένας από τους σημαντικότερους νόμους της θερμοδυναμικής. Αξίζει να αναφέρουμε πως υπάρχουν δύο (2) ισοδύναμες βασικές διατυπώσεις του νόμου αυτού:
1.Κάθε θερμική μηχανή έχει απώλειες ενέργειας.
2.Για τη λειτουργία μιας ψυκτικής μηχανής απαιτείται καταβολή ενέργειας.
Εξετάζοντας τον νόμο με βάση την εντροπία με κάθε μεταβολή που γίνεται στο σύστημα η συνολική εντροπία μεγαλώνει και μόνο στην ιδανική περίπτωση των αντιστρεπτών μεταβολών μένει σταθερή. Ουσιαστικά, ο νόμος αυτός μας δείχνει ότι η θερμότητα δεν μπορεί να περάσει αυθόρμητα από ένα σώμα σ’ ένα άλλο, θερμότερο από το αρχικό.
Τέλος, να αναφέρουμε πως ο 2ος θερμοδυναμικός νόμος πρωτοδιατυπώθηκε το 1865 από τον Γερμανό φυσικό Ρούντολφ Κλαούζιους (Rudolf Julius Emmanuel Clausius, 2 Ιανουαρίου 1822 – 24 Αυγούστου 1888), ο οποίος θεωρείται ο θεμελιωτής της θερμοδυναμικής.Η διατύπωση του 2ου θερμοδυναμικού νόμου οδήγησε σε τεχνολογίες όπως οι κινητήρες εσωτερικής καύσης, η κρυογενετική και οι γεννήτριες.
Περιγραφή του Φαινομένου Κόμπτον
O Κόμπτον και οι συνεργάτες του απέδειξαν ήδη από το 1922 πως η κλασική φυσική δεν μπορούσε να εξηγήσει τη σκέδαση των ακτίνων Χ από τα ηλεκτρόνια. Σύμφωνα με τη συμβατική εξήγηση, το ηλεκτρόνιο ταλαντώνεται όταν οι ακτίνες Χ το χτυπούν. Αμέσως μετά, το ηλεκτρόνιο αποκτά ταχύτητα και αρχίζει να απελευθερώνει ηλεκτρομαγνητική ενέργεια. Ανάλογα με το πόσο καιρό εκτίθεται το ηλεκτρόνιο στην ακτινοβολία και πόσο έντονη είναι αυτή, η ακτινοβολία αυτή θα έχει μια συχνότητα. Ωστόσο, το πείραμα απέδειξε ότι η συχνότητα της σκεδαζόμενης ακτινοβολίας εξαρτάται αποκλειστικά από τη γωνία σκέδασης. Ως εκ τούτου, η συμβατική εξήγηση δεν ήταν σε θέση να εξηγήσει επαρκώς το συγκεκριμένο φαινόμενο.
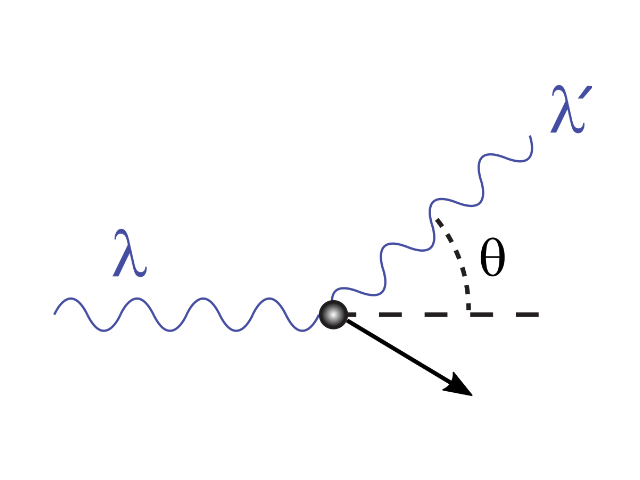
Μετρώντας τα μήκη κύματος και την ένταση των σκεδαζόμενων δεσμών και εκτελώντας το πείραμα σε διάφορες γωνίες σκέδασης, ο Κόμπτον μπόρεσε να εντοπίσει δύο κορυφές στη γραφική παράσταση της έντασης σε σχέση με το μήκος κύματος.
Συγκεκριμένα, η πρώτη κορυφή αντιστοιχούσε σε μήκος κύματος λ, που ήταν το μήκος κύματος της αρχικής δέσμης. Η δεύτερη κορυφή αντιστοιχούσε σε μήκος κύματος λ’, του οποίου η σχέση με τη γωνία σκέδασης φαινόταν από τον εξής τύπο:
Να σημειωθεί πως όπου h η σταθερά δράσεως του Πλάνκ, me η μάζα ηρεμίας του ηλεκτρονίου και c η ταχύτητα του φωτός.
Για τη θεωρητική του εξαγωγή διατυπώθηκαν οι ακόλουθες υποθέσεις:
- Η προσπίπτουσα ηλεκτρομαγνητική ακτινοβολία αποτελείται από φωτόνια με ενέργεια που δίνεται από τον τύπο του Πλανκ (E=hν)
- Τα φωτόνια, όντας σωματίδια, σκεδάζονται από ελαφρώς δέσμια ατομικά ηλεκτρόνια
- Τα ηλεκτρόνια κινούνται με σχετικιστικές ταχύτητες
- Η ενέργεια και η ορμή πριν και μετά την σκέδαση είναι διατηρούμενες ποσότητες
Συνεπώς, ο φαινόμενο αυτό αποτελεί μια από τις πρώτες επιτυχίες της κβαντικής θεωρίας εξαιτίας των παραπάνω παραγόντων.
Η ανακάλυψη της ηλεκτρικής μπαταρίας
Ο Αλεσάντρο Βόλτα, το πλήρες όνομα του οποίου είναι Conte Alessandro Giuseppe Antonio Anastasio Volta, ήταν Ιταλός επιστήμονας. Γεννήθηκε στο Κόμο της Λομβαρδίας στις 18 Φεβρουαρίου 1745 και πέθανε εκεί στις 5 Μαρτίου 1827. Η ανακάλυψη της ηλεκτρικής μπαταρίας του λειτούργησε ως η πρώτη πηγή συνεχούς ρεύματος.
Λίγα λόγια για τον Βόλτα και την ανακάλυψή του
Το 1774, ο Αλεσάντρο Βόλτα διορίστηκε καθηγητής φυσικής στη Βασιλική Σχολή του Κόμο. Η αγάπη του για τον ηλεκτρισμό τον ενέπνευσε να βελτιώσει τον ηλεκτροφόρο, μια μηχανή που παρήγαγε στατικό ηλεκτρισμό, το 1775. Λίγο αργότερα το 1776, ο Βόλτα ανακάλυψε και καθάρισε το αέριο μεθάνιο. Τρία χρόνια αργότερα του ανατέθηκε η έδρα της φυσικής στο Πανεπιστήμιο της Παβίας.
Ο Λουίτζι Γκαλβάνι, φίλος του Βόλτα, ανέφερε το 1791 ότι παράγεται ηλεκτρικό ρεύμα όταν δύο διαφορετικά μέταλλα έρχονται σε επαφή με τους μύες των ποδιών ενός γδαρμένου βατράχου, με αποτέλεσμα το άκρο να συσπάται. Ο Γκαλβάνι θεώρησε ότι αυτό ήταν η ανακάλυψη ενός νέου τύπου ηλεκτρισμού, τον οποίο ονόμασε «ζωικό ηλεκτρισμό», σε ζωντανούς ιστούς.
Ωστόσο, ο Βόλτα πίστευε πως ο βάτραχος απλώς διηύθυνε αυτό που ονόμασε «μεταλλικό ηλεκτρισμό», ένα ρεύμα που ρέει δηλαδή μεταξύ των δύο μετάλλων. Το 1792 ο Βόλτα άρχισε να ερευνά αποκλειστικά με μέταλλα. Μάλιστα, κατά τη διάρκεια της μελέτης και των πειραμάτων του, ο Ιταλός επιστήμονας τοποθετούσε δίσκους από διάφορα μέταλλα στη γλώσσα του για να αισθάνεται το ασθενές ηλεκτρικό ρεύμα που ρέει μεταξύ τους.
Έτσι, ο Αλεσάντρο Βόλτα ανακάλυψε ότι δεν απαιτείται ζωικός ιστός για την παραγωγή ρεύματος. Αξίζει να σημειωθεί πως όταν ο Βόλτα ανακοίνωσε την πρώτη ηλεκτρική μπαταρία το 1800, έβαλε τέλος στη σφοδρή διαμάχη μεταξύ των υποστηρικτών του ζωικού και του μεταλλικού ηλεκτρισμού.
Η μπαταρία του Βόλτα, που συχνά αναφέρεται ως βολταϊκή στήλη (ή αλλιώς βολταϊκός σωρός), αποτελούνταν από εναλλασσόμενους δίσκους ψευδαργύρου και αργύρου (ή χαλκού και κασσίτερου), οι οποίοι χωρίζονταν μεταξύ τους με φύλλα χαρτιού ή υφάσματος βουτηγμένα σε αλατόνερο ή υδροξείδιο του νατρίου.
Το δημιούργημά του πυροδότησε ένα νέο κύμα ηλεκτρικών πειραμάτων, καθώς ήταν μια εύχρηστη, αξιόπιστη πηγή ηλεκτρικού ρεύματος που δεν απαιτούσε επαναφόρτιση. Μέσα σε έξι εβδομάδες από την ανακοίνωση του Βόλτα, οι Άγγλοι ερευνητές Γουίλιαμ Νίκολσον και Άντονι Καρλίσλι χρησιμοποίησαν έναν σωρό Βόλτα για να μετατρέψουν το νερό σε υδρογόνο και οξυγόνο. Αυτή η ανακάλυψη της ηλεκτρόλυσης – η διαδικασία με την οποία ένα ηλεκτρικό ρεύμα προκαλεί μια χημική αντίδραση – οδήγησε στην ανάπτυξη του τομέα της ηλεκτροχημείας.
Να αναφέρουμε επίσης πως ο Ναπολέων έκανε τον Βόλτα κόμη και γερουσιαστή του βασιλείου της Λομβαρδίας, καθώς ο Ιταλός επιστήμονας παρουσίασε μπροστά του την παραγωγή ηλεκτρικού ρεύματος από την μπαταρία του το 1801 στο Παρίσι. Εν συνεχεία, το 1815, διορίστηκε διευθυντής της φιλοσοφικής σχολής του Πανεπιστημίου της Πάντοβα από τον Αυστριακό αυτοκράτορα Φραγκίσκο Α. Τέλος, το 1881, ο Βόλτα συνέβαλε στην έμπνευση για τη δημιουργία του βολτ – μιας μέτρησης της ηλεκτροκινητικής δύναμης που τροφοδοτεί τον ηλεκτρισμό.
Υπόθεση P versus NP: Υπάρχει μια ιδανική διάταξη συνδαιτυμόνων;
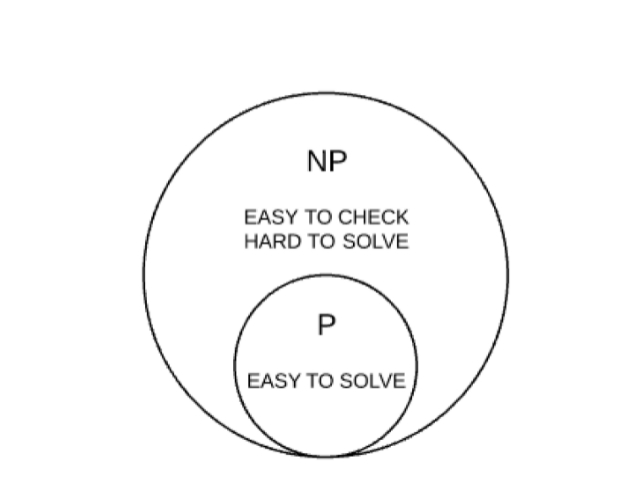
Η υπόθεση αυτή παραμένει άλυτη εδώ και 30 χρόνια. Το πρόβλημα αυτού του τύπου, «Ρ versus ΝΡ» -όπως λέγεται- εμφανίστηκε τη δεκαετία του 1970, όταν το διατύπωσαν οι Stephen Cook και Leonid Levin . Σύμφωνα με αυτή την υπόθεση, το Ρ σημαίνει εύκολο να βρεθεί λύση και το ΝΡ σημαίνει εύκολο να ελεγχθεί.
Η υπόθεση αυτή έχει να κάνει με το αν όντως υπάρχουν προβλήματα τα οποία είναι εύκολο να ελεγχθούν αλλά πρακτικά αδύνατο να λυθούν με άμεσες αλγοριθμικές διαδικασίες. Για παράδειγμα: Ας υποθέσουμε ότι πρόκειται να γίνει ένα εορταστικό τραπέζι και στα χέρια μας έχουμε 2 λίστες. Μια λίστα με 500 πιθανούς καλεσμένους και μια άλλη με ζεύγη αυτών των ανθρώπων που δεν πρέπει να εμφανιστούν στον τελικό κατάλογο των καλεσμένων. Είναι εύκολο να ελέγξουμε αν μια συγκεκριμένη λίστα 100 ατόμων, από 500 πιθανούς καλεσμένους, ικανοποιεί το κριτήριό μας να μην υπάρχουν ασύμβατα μεταξύ τους ζευγάρια στο τραπέζι. Το να δημιουργήσουμε όμως εμείς μια τέτοια λίστα από τους 500 πιθανούς καλεσμένους είναι τόσο δύσκολο που μοιάζει να είναι πρακτικά αδύνατο. Μάλιστα, ο αριθμός των εναλλακτικών τρόπων που μπορούμε να διαλέξουμε 100 καλεσμένους από τους 500 είναι μεγαλύτερος από το σύνολο των ατόμων που υπάρχουν στο σύμπαν, γι’ αυτό και στη λύση αυτού του προβλήματος δεν θα μπορούσε να βοηθήσει ούτε ο ισχυρότερος υπολογιστής.
Για προβλήματα όπως το παραπάνω, κανείς μέχρι σήμερα δεν έχει καταφέρει να δείξει ότι η λύση τους δεν είναι εφικτή με κατάλληλη προγραμματιστική μέθοδο.
Αποστολή Dart
Στις 27 Σεπτεμβρίου η NASA έφερε εις πέρας μια πολύ απαιτητική αποστολή που στην ουσία αποτελεί μια πρόβα πλανητικής άμυνας στην περίπτωση που παρουσιαστεί μια μέρα ο κίνδυνος σύγκρουσης ενός αστεροειδούς με τη Γη.
Ποιός το έκανε; 2+1 γρίφοι για δυνατούς λύτες
Οι γρίφοι και οι σπαζοκεφαλιές ανέκαθεν δημιουργούσαν μια έντονη περιέργεια σε μικρούς και μεγάλους. Και σίγουρα, είναι μια δραστηριότητα που οξύνει την φαντασία, το μυαλό και την κριτική σκέψη. Παρακάτω υπάρχουν 3 γρίφοι, στους οποίους καλείσαι να δώσεις λύσεις. Μπορείς όμως;
Συγκεκριμένα:
- Μια μαθήτρια βρίσκεται δολοφονημένη την πρώτη μέρα του σχολείου. Οι ύποπτοι είναι τέσσερις: Ο Ντιν ισχυρίστηκε πως βρισκόταν όλη μέρα στο γραφείο του. Η καθηγήτρια των μαθηματικών είπε πως ήταν στην τάξη και έδινε τους βαθμούς των εξετάσεων στους μαθητές. Ο Πέον είπε πως παρέδιδε τα γράμματα και ο Τζάνιτορ πως καθάριζε τις τουαλέτες του πρώτου ορόφου. Ποιος λέει ψέματα;
- Ένας άντρας βρίσκεται δολοφονημένος στο σπίτι του, η αστυνομία βρήκε τρεις ύποπτους, τον Όλιβερ, τον Τζέισον και τον Άνταμ, που είχαν κίνητρο και περιθώριο για να διαπράξουν το φόνο. H αστυνομία βρήκε ένα σημείωμα γραμμένο από το θύμα. Τι προσπαθούσε να μας πει;
- Μια γυναίκα βρέθηκε νεκρή στο σπίτι της, ενώ εκεί βρίσκονταν τέσσερα άτομα. Ο ένοχος άφησε πολλά στοιχεία, από ένα σημείωμα σε έξι διαφορετικά σημεία του σπιτιού που έγραφαν τα στοιχεία είναι όπου βρίσκονται τα σημειώματα. Μπορείτε να βρείτε τον δολοφόνο;
Δες το βίντεο για να έχεις την πλήρη εικόνα για κάθε γρίφο: https://www.youtube.com/watch?v=4-KbOe05CQg&t=1s
Λύσεις:
- Ένοχη είναι η δασκάλα των μαθηματικών καθώς δεν γίνεται να παρέδωσε αποτελέσματα διαγωνίσματος την πρώτη μέρα του σχολείου.
- Το θύμα αποκάλυψε το όνομα του ένοχου. Κάθε νούμερο συμβολίζει έναν μήνα, τα αρχικά δίνουν το όνομα του ενόχου, δηλαδή του Τζέισον.
- Στην ίδια λογική, το αρχικό γράμμα κάθε μέρος του σπιτιού αποκαλύπτει ένα γράμμα από το όνομα του ενόχου, δηλαδή του Μάρκους.
Τα κατάφερες;
Στήβεν Χόκινγκ: Λίγα λόγια για τον σπουδαίο θεωρητικό φυσικό και κοσμολόγο
Ο Στήβεν Γουίλιαμ Χόκινγκ γεννήθηκε στις 8 Ιανουαρίου 1942 στην Οξφόρδη και απεβίωσε στις 14 Μαρτίου 2018 στο Κέιμπριτζ. Ο ίδιος καταξιώθηκε ως θεωρητικός φυσικός, αστροφυσικός, κοσμολόγος, συγγραφέας, ενώ διετέλεσε και Διευθυντής Ερευνών στο Κέντρο Θεωρητικής Κοσμολογίας στο Πανεπιστήμιο του Κέμπριτζ.
Με πλούσιο επιστημονικό έργο, ο Στήβεν Χόκινγκ το 1971 διατύπωσε μια θεωρία για τις μαύρες τρύπες, βασισμένη τόσο στη θεωρία της σχετικότητας, όσο και στην κβαντομηχανική. Συγκεκριμένα, έκανε την υπόθεση για τον σχηματισμό, μετά τη Μεγάλη Έκρηξη (Big Bang), πολυάριθμων αντικειμένων συνολικής μάζας της τάξης των 10⁹ τόνων, ο όγκος των οποίων, όμως, είναι συγκρίσιμος με αυτόν του πρωτονίου. Τα σώματα αυτά, γνωστά ως μικροσκοπικές μαύρες τρύπες, παρουσιάζουν την ιδιομορφία ότι η τεράστια μάζα και βαρύτητά τους μπορούν να μελετηθούν μόνο με βάση τους νόμους της σχετικότητας, ενώ οι μικροσκοπικές διαστάσεις τους απαιτούν επίσης για την περιγραφή τους και την εφαρμογή των νόμων της κβαντομηχανικής.
Το 1974, ο Χόκινγκ ανέπτυξε την άποψη ότι, σύμφωνα με τις προβλέψεις της κβαντομηχανικής, οι μαύρες τρύπες εκπέμπουν υποατομικά σωματίδια, διαδικασία που συνεχίζεται έως ότου εξαντληθούν τα ενεργειακά τους αποθέματα, οπότε και εκρήγνυνται.
Η σημαντική συμβολή του Χόκινγκ στη Φυσική του απέφερε πολλές διακρίσεις. Το 1974, σε ηλικία μόλις 32 ετών, η Βασιλική Ακαδημία Επιστημών της Μεγάλης Βρετανίας τον εξέλεξε ως έναν από τα νεότερα μέλη της. Στη συνέχεια, το 1977 έγινε καθηγητής της Βαρυτικής Φυσικής στο Πανεπιστήμιο του Κέiμπριτζ, ενώ δύο χρόνια αργότερα καθηγητής Μαθηματικών στο ίδιο πανεπιστήμιο, σε μία έδρα που παλαιότερα κατείχε ο Νεύτων.
Ασχολήθηκε επίσης με τη μελέτη των ιδιαίτερων προβλημάτων του χωροχρόνου και συνέγραψε το μπεστ-σέλερ «Το χρονικό του χρόνου» (1988), το οποίο εξηγεί με απλό τρόπο τις βασικές αρχές της κοσμολογίας. Το βιβλίο έγινε παγκόσμιο μπεστ-σέλερ, μεταφράστηκε σε 40 γλώσσες κι έχει πουλήσει πάνω 25 εκατομμύρια αντίτυπα.
Αν και δεν κατάφερε, ή δεν πρόλαβε, να πάρει το Νόμπελ, είχε τιμηθεί με πολλά άλλα σημαντικά βραβεία (Αϊνστάιν, Βολφ, Κόπλεϊ κ.ά.). Επίσης, αρεσκόταν να βάζει επιστημονικά στοιχήματα με άλλους φυσικούς, αν και είχε μία τάση να τα χάνει, όπως για παράδειγμα όταν το 2012 έχασε 100 δολάρια, επειδή είχε στοιχηματίσει ότι ποτέ δεν θα ανακαλυπτόταν το μποζόνιο του Χιγκς, το οποίο βρέθηκε στο CERN λίγο μετά.
Στο μεγαλύτερο μέρος της ζωής του ο Στήβεν Χόκινγκ παρέμεινε καθηλωμένος σε αναπηρικό αμαξίδιο, εξαιτίας μιας ανίατης νευρολογικής νόσου. Επιπρόσθετα, για πολλά χρόνια μιλούσε με συνθετική φωνή, αφού υποβλήθηκε και σε τραχειοστομία εξαιτίας μιας πνευμονίας.
Η ζωή του σπουδαίου αυτού ανθρώπου μάλιστα, αποτυπώθηκε και στη μεγάλη οθόνη, με πιο γνωστή την ταινία που φέρει τον τίτλο «Η θεωρία των πάντων» (The Theory of Everything, 2014) του σκηνοθέτη Τζέιμς Μαρς. Τον ρόλο του θεωρητικού φυσικού ενσάρκωσε ο ταλαντούχος Άγγλος ηθοποιός Έντι Ρέντμεϊν Όσκαρ Ά ανδρικού ρόλου). Πέρα από το Όσκαρ, ο ηθοποιός για την ερμηνεία του έλαβε και τα εύσημα του ίδιου του Χόκινγκ, ο οποίος είχε δηλώσει: «Μερικές φορές νόμιζα ότι ήμουν εγώ» είχε δηλώσει ο Χόκινγκ.
Δείτε εδώ το τρέιλερ της βραβευμένης ταινίας: https://www.youtube.com/watch?v=Pac8A3-ti48
5 γρίφοι για να οξύνετε το μυαλό και την φαντασία σας
Οι γρίφοι ανέκαθεν έκρυβαν μια γοητεία για τους ανθρώπους όλων των ηλικιών, καθώς οξύνουν το μυαλό και τη φαντασία. Παρακάτω θα βρείτε 5 γρίφους για να «παιδέψετε» ευχάριστα και δημιουργικά το μυαλό σας.
- Η Μαίρη πήγε στην αστυνομία και ισχυρίστηκε ότι δεν βρίσκει το κουτί της με τα κοσμήματα. Η αστυνομία πήγε στο σπίτι της Μαίρης και δεν παρατήρησε κάποιο σημάδι διάρρηξης. Μάλιστα, το σαλόνι ήταν τακτοποιημένο και εντελώς καθαρό. Ωστόσο ένα παράθυρο ήταν σπασμένο χωρίς όμως να υπάρχουν γυαλιά στο πάτωμα. Η αστυνομία συνέλαβε τη Μαίρη για απάτη. Πώς ήξερε η αστυνομία ότι η Μαίρη έλεγε ψέματα;
- Ο Μάνος είπε στη Νικολέττα, «Αυτό το χαρτονόμισμα των 5 ευρώ δεν είναι αυτό που άφησες πριν στο τραπέζι. Το βρήκα ανάμεσα στις σελίδες 15 και 16 του Χάρυ». Η Νικολέττα απάντησε, «Λες ψέματα και μπορώ να το αποδείξω». Πώς ήξερε η Νικολέττα ότι ο Μάνος έλεγε ψέματα;
- Ο Γιώργος βρίσκεται στη φυλακή. Το πάτωμα στο κελί του αποτελείται από χώμα και πολύ ψηλά υπάρχει ένα παράθυρο το οποίο δεν μπορεί να φτάσει. Το μόνο αντικείμενο στο κελί του είναι ένα φτυάρι. Ο Γιώργος έχει βάλει στόχο να βγει μέσα σε 2 μέρες από τη φυλακή, οπότε δε μπορεί να σκάψει μια σήραγγα καθώς αυτό θα του πάρει περισσότερο. Πώς θα καταφέρει να βγει;
- Μια κρύα μέρα του χειμώνα, ένας άντρας κοίταξε από το παράθυρο και είδε έναν άνθρωπο να στέκεται στην αυλή του. Ο άνθρωπος αυτός έμεινε για πολλές εβδομάδες στην αυλή και ο ιδιοκτήτης του σπιτιού δεν θορυβήθηκε καθόλου. Κάποια στιγμή, ο άνθρωπος αυτός έφυγε από την αυλή. Ποιος ήταν αυτός ο άνθρωπος;
- Ένας άνδρας βρίσκεται σε ένα στρατόπεδο αιχμάλωτος. Το στρατόπεδο αυτό είναι πάνω σε μια βραχονησίδα όπου δεν επιτρέπεται ούτε να μπει ούτε να βγει κανείς. Έχει πρόσβαση σε μια γέφυρα που ενώνει το στρατόπεδο με την πόλη, η οποία χρειάζεται 3 λεπτά για να τη διασχίσει κάποιος ολόκληρη. Όμως, ο φρουρός βγαίνει κάθε 1 λεπτό από ένα φυλάκιο και ελέγχει τη γέφυρα. Ο φρουρός δεν έχει ξαναδεί το πρόσωπο του αιχμαλώτου. Υπάρχει τρόπος να καταφέρει ο αιχμάλωτος να ξεφύγει;
Απαντήσεις
1. Το παράθυρο του σαλονιού είχε σπάσει από μέσα γιατί δεν υπήρχαν γυαλιά στο πάτωμα. Εάν είχε σπάσει από έξω θα βρίσκονταν γυαλιά στο πάτωμα του σαλονιού.
2. Όπως όλα τα βιβλία, έτσι και ο Χάρυ Πότερ έχει τους μονούς αριθμούς στη δεξιά σελίδα. Έτσι, οι σελίδες 15 και 16 είναι μια μόνο σελίδα μπρος πίσω, και δεν θα μπορούσε να έχει βρεθεί κάτι ανάμεσα σε αυτές.
3. Ο Γιώργος πρέπει να χρησιμοποιήσει το φτυάρι για να φτιάξει ένα ύψωμα από χώμα κάτω από το παράθυρο ώστε να ανέβει πάνω σε αυτό και φτάνοντας στο παράθυρο να ξεφύγει από το κελί του.
4. Ήταν ένας χιονάνθρωπος
5. Ναι, αν παραμονεύσει τον φρουρό. Μόλις ο φρουρός μπει στο φυλάκιο, ο άνδρας πρέπει να αρχίσει να περπατάει πάνω στη γέφυρα για 1 λεπτό. Όταν συμπληρωθεί το 1 λεπτό και ξαναβγεί ο φρουρός, ο άντρας πρέπει να αρχίσει να περπατάει προς την αντίθετη φορά. Έτσι, ο φρουρός που θα δει κάποιον να περπατάει προς το στρατόπεδο θα τον σταματήσει και θα του πει να γυρίσει πίσω, αφού δεν επιτρέπεται η είσοδος στο στρατόπεδο.
Βρήκατε τις απαντήσεις στους παραπάνω γρίφους;
Και όμως γυρίζει…
Ο Γαλιλαίος ήταν Ιταλός μελετητής που ασχολήθηκε με την αστρονομία, τη φυσική, τη φιλοσοφία και τα μαθηματικά, Η έρευνά του συνέβαλε σημαντικά στην ανάπτυξη της θεωρίας του ηλιοκεντρισμού, δηλαδή της θεωρίας ότι η γη γυρίζει γύρω από τον ήλιο, έναντι της θεωρίας του γεωκεντρισμού η οποία υποστήριζε ότι η γη είναι σταθερή και ο ήλιος γυρίζει γύρω από αυτή. Η επιμονή του σε αυτή τη θεωρία είχε ως αποτέλεσμα την καταδίκη του σε ισόβια φυλάκιση από το Ιεροδικείο της Ρώμης το 1633.
O Γαλιλαίος δεν ήταν ο πρώτος που υποστήριξε, ότι η γη δεν είναι το κέντρο του κόσμου. Είχε προηγηθεί ο Κοπέρνικος, ο οποίος γλίτωσε από την Καθολική Εκκλησία επειδή στην πρώτη σελίδα του έργου του σημείωνε, ότι η θεωρία του δεν περιέγραφε απόλυτα τους ουρανούς, αλλά ότι αποτελούσε μια απλούστερη μαθηματική μέθοδο μέτρησης των αστεριών και των πλανητών σε αντίθεση με το παλαιότερο Πτολεμαϊκό σύστημα που χρησιμοποιούνταν τότε.
Μη ακολουθώντας παρόμοιες διπλωματικές μεθόδους, ο Γαλιλαίος αφιερώθηκε στο να πείσει τον κόσμο ότι η γη γυρίζει γύρω από τον ήλιο. Παρά τις συνεχείς παροτρύνσεις των φίλων του από την πλευρά της Εκκλησίας να σταματήσει να υποστηρίζει τον Κοπερνικανισμό, ο ίδιος γινόταν ολοένα και πιο προκλητικός. Μάλιστα, σε πολλές περιπτώσεις χρησιμοποιούσε εδάφια από την Βίβλο προκειμένου να δείξει ότι η μέχρι τότε αντίληψη πως η γη είναι ακίνητη είναι λάθος.
Σύντομα, η επιείκεια της Εκκλησίας προς το πρόσωπο του Γαλιλαίου εξαντλήθηκε. Η επίσημη απόφαση των θεολόγων του Βατικανού χαρακτήριζε τη θεωρία του Γαλιλαίου ανόητη και άκρως αιρετική. Η κυκλοφορία του βιβλίου του απαγορεύτηκε και ο Γαλιλαίος αναγκάστηκε να αποκηρύξει το έργο του. Παρόλα αυτά, ο θρύλος λέει ότι ο Γαλιλαίος φεύγοντας από την Ιερά Εξέταση αναφώνησε ” Και όμως γυρίζει”.