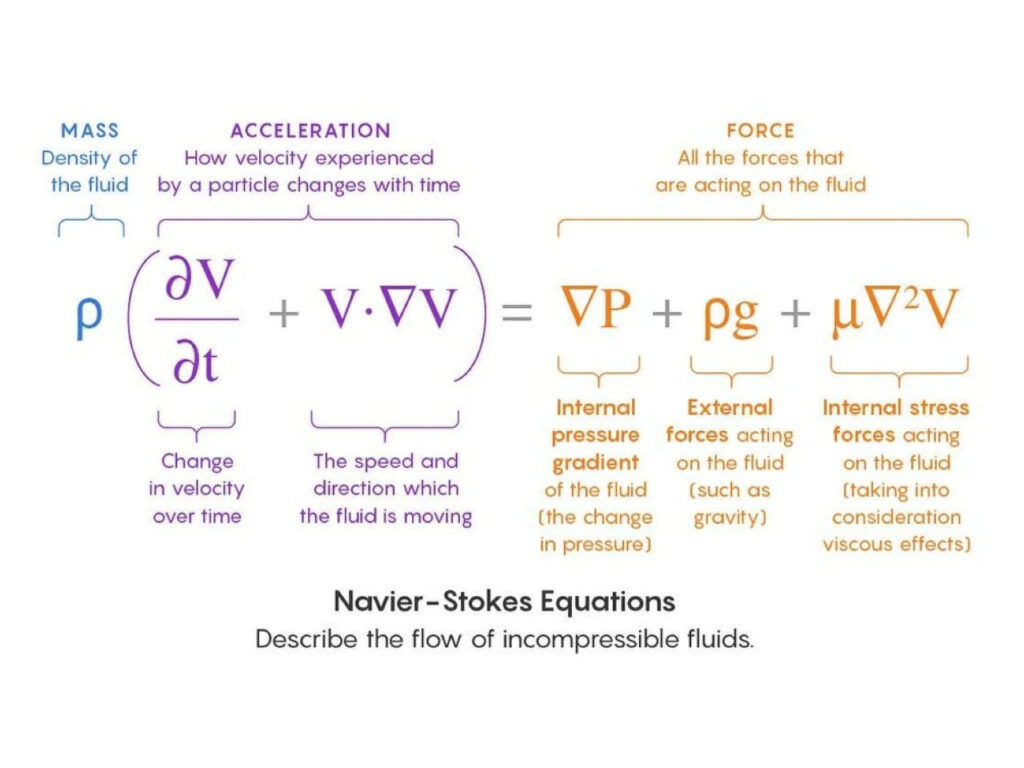
Οι εξισώσεις Navier-Stokes είναι ένα σύνολο μερικών διαφορικών εξισώσεων που περιγράφουν την κίνηση των ρευστών. Οι συγκεκριμένες εξισώσεις πήραν το όνομά τους από τον Γάλλο μαθηματικό και φυσικό Κλοντ-Λουί Ναβιέ (Claude-Louis Navier) και τον Ιρλανδό μαθηματικό και φυσικό George Gabriel Stokes (Τζορτζ Γκάμπριελ Στόουκς). Αξίζει να αναφέρουμε πως αυτές οι εξισώσεις περιγράφουν τη διατήρηση της μάζας και της ορμής σε ένα ρευστό, λαμβάνοντας υπόψη τις επιδράσεις του ιξώδους και των εξωτερικών δυνάμεων. Μπορούν να γραφούν σε διανυσματική μορφή ως εξής:
∂ρ/∂t + ∇-(ρv) = 0
ρ (∂v/∂t + v-∇v) = -∇p + ∇-τ + f
Όπου:
● ρ είναι η πυκνότητα του ρευστού,
● v είναι το διάνυσμα ταχύτητας του ρευστού,
● p είναι η πίεση,
● τ είναι ο τανυστής ιξώδους τάσης,
● f είναι κάθε εξωτερική δύναμη που ασκείται στο ρευστό, όπως η βαρύτητα¨.
Η πρώτη εξίσωση είναι η εξίσωση συνέχειας, η οποία δηλώνει ότι ο ρυθμός μεταβολής της πυκνότητας σε οποιοδήποτε στοιχείο του ρευστού είναι ίσος με την αρνητική απόκλιση της ταχύτητας του ρευστού. Η δεύτερη εξίσωση είναι η εξίσωση ορμής, η οποία δηλώνει ότι ο ρυθμός μεταβολής της ορμής σε οποιοδήποτε στοιχείο του ρευστού είναι ίσος με το άθροισμα των δυνάμεων που ασκούνται στο στοιχείο αυτό.
Οι εξισώσεις Navier-Stokes είναι εξαιρετικά μη γραμμικές και δύσκολα επιλύονται αναλυτικά, ακόμη και για απλές γεωμετρίες και οριακές συνθήκες. Μάλιστα, έχουν σημαντικές εφαρμογές σε πολλούς τομείς, όπως η δυναμική των ρευστών, η αεροδυναμική και η πρόβλεψη του καιρού.