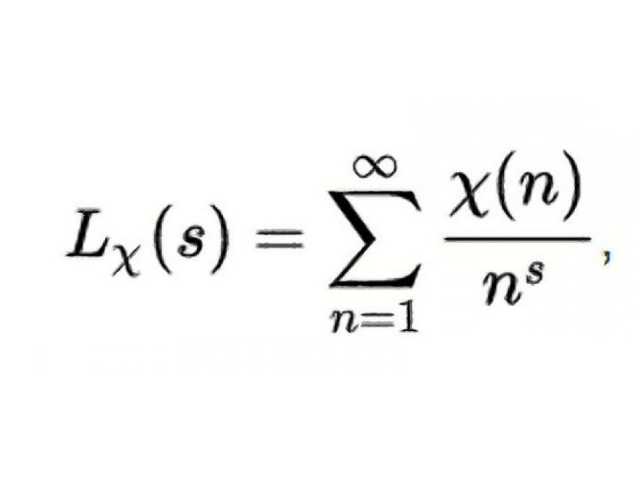Home » Articles posted by e-diakrisi (Page 6)
Author Archives: e-diakrisi
5 γρίφοι για να οξύνετε το μυαλό και την φαντασία σας
Οι γρίφοι ανέκαθεν έκρυβαν μια γοητεία για τους ανθρώπους όλων των ηλικιών, καθώς οξύνουν το μυαλό και τη φαντασία. Παρακάτω θα βρείτε 5 γρίφους για να «παιδέψετε» ευχάριστα και δημιουργικά το μυαλό σας.
- Η Μαίρη πήγε στην αστυνομία και ισχυρίστηκε ότι δεν βρίσκει το κουτί της με τα κοσμήματα. Η αστυνομία πήγε στο σπίτι της Μαίρης και δεν παρατήρησε κάποιο σημάδι διάρρηξης. Μάλιστα, το σαλόνι ήταν τακτοποιημένο και εντελώς καθαρό. Ωστόσο ένα παράθυρο ήταν σπασμένο χωρίς όμως να υπάρχουν γυαλιά στο πάτωμα. Η αστυνομία συνέλαβε τη Μαίρη για απάτη. Πώς ήξερε η αστυνομία ότι η Μαίρη έλεγε ψέματα;
- Ο Μάνος είπε στη Νικολέττα, «Αυτό το χαρτονόμισμα των 5 ευρώ δεν είναι αυτό που άφησες πριν στο τραπέζι. Το βρήκα ανάμεσα στις σελίδες 15 και 16 του Χάρυ». Η Νικολέττα απάντησε, «Λες ψέματα και μπορώ να το αποδείξω». Πώς ήξερε η Νικολέττα ότι ο Μάνος έλεγε ψέματα;
- Ο Γιώργος βρίσκεται στη φυλακή. Το πάτωμα στο κελί του αποτελείται από χώμα και πολύ ψηλά υπάρχει ένα παράθυρο το οποίο δεν μπορεί να φτάσει. Το μόνο αντικείμενο στο κελί του είναι ένα φτυάρι. Ο Γιώργος έχει βάλει στόχο να βγει μέσα σε 2 μέρες από τη φυλακή, οπότε δε μπορεί να σκάψει μια σήραγγα καθώς αυτό θα του πάρει περισσότερο. Πώς θα καταφέρει να βγει;
- Μια κρύα μέρα του χειμώνα, ένας άντρας κοίταξε από το παράθυρο και είδε έναν άνθρωπο να στέκεται στην αυλή του. Ο άνθρωπος αυτός έμεινε για πολλές εβδομάδες στην αυλή και ο ιδιοκτήτης του σπιτιού δεν θορυβήθηκε καθόλου. Κάποια στιγμή, ο άνθρωπος αυτός έφυγε από την αυλή. Ποιος ήταν αυτός ο άνθρωπος;
- Ένας άνδρας βρίσκεται σε ένα στρατόπεδο αιχμάλωτος. Το στρατόπεδο αυτό είναι πάνω σε μια βραχονησίδα όπου δεν επιτρέπεται ούτε να μπει ούτε να βγει κανείς. Έχει πρόσβαση σε μια γέφυρα που ενώνει το στρατόπεδο με την πόλη, η οποία χρειάζεται 3 λεπτά για να τη διασχίσει κάποιος ολόκληρη. Όμως, ο φρουρός βγαίνει κάθε 1 λεπτό από ένα φυλάκιο και ελέγχει τη γέφυρα. Ο φρουρός δεν έχει ξαναδεί το πρόσωπο του αιχμαλώτου. Υπάρχει τρόπος να καταφέρει ο αιχμάλωτος να ξεφύγει;
Απαντήσεις
1. Το παράθυρο του σαλονιού είχε σπάσει από μέσα γιατί δεν υπήρχαν γυαλιά στο πάτωμα. Εάν είχε σπάσει από έξω θα βρίσκονταν γυαλιά στο πάτωμα του σαλονιού.
2. Όπως όλα τα βιβλία, έτσι και ο Χάρυ Πότερ έχει τους μονούς αριθμούς στη δεξιά σελίδα. Έτσι, οι σελίδες 15 και 16 είναι μια μόνο σελίδα μπρος πίσω, και δεν θα μπορούσε να έχει βρεθεί κάτι ανάμεσα σε αυτές.
3. Ο Γιώργος πρέπει να χρησιμοποιήσει το φτυάρι για να φτιάξει ένα ύψωμα από χώμα κάτω από το παράθυρο ώστε να ανέβει πάνω σε αυτό και φτάνοντας στο παράθυρο να ξεφύγει από το κελί του.
4. Ήταν ένας χιονάνθρωπος
5. Ναι, αν παραμονεύσει τον φρουρό. Μόλις ο φρουρός μπει στο φυλάκιο, ο άνδρας πρέπει να αρχίσει να περπατάει πάνω στη γέφυρα για 1 λεπτό. Όταν συμπληρωθεί το 1 λεπτό και ξαναβγεί ο φρουρός, ο άντρας πρέπει να αρχίσει να περπατάει προς την αντίθετη φορά. Έτσι, ο φρουρός που θα δει κάποιον να περπατάει προς το στρατόπεδο θα τον σταματήσει και θα του πει να γυρίσει πίσω, αφού δεν επιτρέπεται η είσοδος στο στρατόπεδο.
Βρήκατε τις απαντήσεις στους παραπάνω γρίφους;
Και όμως γυρίζει…
Ο Γαλιλαίος ήταν Ιταλός μελετητής που ασχολήθηκε με την αστρονομία, τη φυσική, τη φιλοσοφία και τα μαθηματικά, Η έρευνά του συνέβαλε σημαντικά στην ανάπτυξη της θεωρίας του ηλιοκεντρισμού, δηλαδή της θεωρίας ότι η γη γυρίζει γύρω από τον ήλιο, έναντι της θεωρίας του γεωκεντρισμού η οποία υποστήριζε ότι η γη είναι σταθερή και ο ήλιος γυρίζει γύρω από αυτή. Η επιμονή του σε αυτή τη θεωρία είχε ως αποτέλεσμα την καταδίκη του σε ισόβια φυλάκιση από το Ιεροδικείο της Ρώμης το 1633.
O Γαλιλαίος δεν ήταν ο πρώτος που υποστήριξε, ότι η γη δεν είναι το κέντρο του κόσμου. Είχε προηγηθεί ο Κοπέρνικος, ο οποίος γλίτωσε από την Καθολική Εκκλησία επειδή στην πρώτη σελίδα του έργου του σημείωνε, ότι η θεωρία του δεν περιέγραφε απόλυτα τους ουρανούς, αλλά ότι αποτελούσε μια απλούστερη μαθηματική μέθοδο μέτρησης των αστεριών και των πλανητών σε αντίθεση με το παλαιότερο Πτολεμαϊκό σύστημα που χρησιμοποιούνταν τότε.
Μη ακολουθώντας παρόμοιες διπλωματικές μεθόδους, ο Γαλιλαίος αφιερώθηκε στο να πείσει τον κόσμο ότι η γη γυρίζει γύρω από τον ήλιο. Παρά τις συνεχείς παροτρύνσεις των φίλων του από την πλευρά της Εκκλησίας να σταματήσει να υποστηρίζει τον Κοπερνικανισμό, ο ίδιος γινόταν ολοένα και πιο προκλητικός. Μάλιστα, σε πολλές περιπτώσεις χρησιμοποιούσε εδάφια από την Βίβλο προκειμένου να δείξει ότι η μέχρι τότε αντίληψη πως η γη είναι ακίνητη είναι λάθος.
Σύντομα, η επιείκεια της Εκκλησίας προς το πρόσωπο του Γαλιλαίου εξαντλήθηκε. Η επίσημη απόφαση των θεολόγων του Βατικανού χαρακτήριζε τη θεωρία του Γαλιλαίου ανόητη και άκρως αιρετική. Η κυκλοφορία του βιβλίου του απαγορεύτηκε και ο Γαλιλαίος αναγκάστηκε να αποκηρύξει το έργο του. Παρόλα αυτά, ο θρύλος λέει ότι ο Γαλιλαίος φεύγοντας από την Ιερά Εξέταση αναφώνησε ” Και όμως γυρίζει”.
5+2 σπαζοκεφαλιές για… κοφτερά μυαλά!
- Τέσσερις άνδρες μπορούν να φτιάξουν τέσσερις βάρκες σε τέσσερις ημέρες. Πόσος χρόνος χρειάζεται για να φτιάξει ένας άνδρας μία βάρκα;
- Δοκιμάστε τη μνήμη σας: Τρεις άνδρες και οι γυναίκες τους και ένας χήρος πήραν μια μέρα το αυτοκίνητο για να πάνε εκδρομή. Έπειτα από δέκα χιλιόμετρα δρόμο, συνάντησαν δύο άντρες και ένα παιδί σε ένα άλλο αυτοκίνητο, το οποίο είχε χαλάσει. «Τι ατυχία», είπε ένας από τους επιβαίνοντες. Λίγες ώρες μετά, έφτασαν στον προορισμό τους και είδαν εκεί έναν άνδρα και το παιδί του. Πόσα άτομα αναφέρονται συνολικά στην ιστορία;
- Τι είναι πιο βαρύ, το γάλα ή η σαντιγύ;
- Εάν ένα ρολόι σταματά για ένα λεπτό κάθε δέκα λεπτά, πόσα λεπτά θα χρειαστούν για να ολοκληρώσει ο λεπτοδείκτης μία πλήρη περιστροφή;
- Ένας άνδρας έμενε μόνος σε ένα σπίτι. Μπορεί κανείς να μπει στο σπίτι μόνο από την πόρτα ή ένα από τα πέντε παράθυρα. Αφού βεβαιώθηκε ότι δεν υπάρχει κανείς στο σπίτι, ο άνδρας ένα απόγευμα έφυγε από το σπίτι. Όταν επέστρεψε, τα παράθυρα ήταν σφραγισμένα και τα τζάμια δεν ήταν σπασμένα και η πόρτα δεν είχε παραβιαστεί, βρήκε όμως μέσα στο σπίτι έναν κλέφτη. Ο κλέφτης δεν είχε κλειδί ούτε παραβίασε την κλειδαριά, πώς μπήκε στο σπίτι;
- Εάν 1,5 κότα γεννάει 1,5 αυγό σε 1,5 μέρα, πόσα αυγά θα έχουμε από 7 κότες σε 6 μέρες;
- Ο πατέρας μου είναι αδερφός της αδερφής σου. Τι συγγένεια έχουμε; Είμαι ξάδερφος, ανιψιός, γιος ή θείος σου;
Απαντήσεις
- Τέσσερις ημέρες
- 12 άτομα
- Η σαντιγύ, γιατί η σαντιγύ επιπλέει σε ένα ρόφημα
- 65 λεπτά
- Μπήκε από την πόρτα, την οποία ο άνδρας δεν είχε κλειδώσει
- 28 αυγά
- Είμαι ανιψιός σου
Η υπόθεση του Riemann
Πρόσφατα, λύθηκαν δύο δύσκολα μαθηματικά προβλήματα άλυτα για δεκάδες χρόνια. Πρόκειται για την Εικασία του Poincare που επαληθεύτηκε από τον Ρώσο Grigori Perelman και την απεικόνιση μιας τεράστιας και πολύπλοκης μαθηματικής δομής η οποία έχει 248 διαστάσεις και αποκαλείται Ε8, από μια διεθνή ομάδα μαθηματικών.
Η υπόθεση του Riemann, ότι υπάρχει συστηματικότητα στην κατανομή των πρώτων αριθμών, παραμένει άλυτη εδώ και 148 χρόνια. Η ακολουθία των πρώτων αριθμών αρχίζει με τους 2,3, 5, 7 και 11. Όσο προχωράει κανείς στην ακολουθία, η συχνότητα τους μειώνεται, αλλά η κατανομή τους δεν παύει να παρουσιάζει μια συστηματοποίηση, που είναι γνωστή εδώ και αιώνες. Υπάρχουν, ωστόσο, μικρές παρεκκλίσεις, και το 1859 ο Bemhard Riemann υπέθεσε ότι θα μπορούσε να τις περιγράψει ακριβώς, αν κατάφερνε να αποδείξει την ύπαρξη μιας ξεχωριστής ιδιότητας για τις τιμές που μηδενίζουν μια συγκεκριμένη συνάρτηση. Η υπόθεση έχει επαληθευτεί για τις πρώτες 1.500.000.001 λύσεις, αλλά εξακολουθεί να λείπει η τελική απόδειξη.
Λίγα λόγια για την σπουδαία μαθηματικό Μαρί-Σοφία Ζερμέν
Λίγα λόγια για τον Ευκλείδη
Ο Ευκλείδης ήταν Έλληνας μαθηματικός από την Αλεξάνδρεια, που δίδαξε και πέθανε στην Αλεξάνδρεια της Αιγύπτου, κατά τη διάρκεια της περιόδου βασιλείας του Πτολεμαίου Α΄ (323 π.Χ. – 283 π.Χ.). Γεννήθηκε περίπου το 330 π.Χ. και πέθανε το 275 π.Χ. ή το 270 π.Χ. Σπούδασε στην Αθήνα, στην Ακαδημία του Πλάτωνα, όπου και διακρίθηκε για τις μαθηματικές του εργασίες. Η αλήθεια είναι, πως για τη ζωή του Ευκλείδη ελάχιστα είναι γνωστά και από αυτά λίγα είναι εξακριβωμένα. Ωστόσο, το σίγουρο είναι πως ο Ευκλείδης έχει μείνει γνωστός μέχρι και σήμερα ως ο «πατέρας» της Γεωμετρίας, καθώς είναι ο πρώτος που έδωσε στη Γεωμετρία μια ανυπέρβλητη λογική αυστηρότητα με την εισαγωγή της αξιωματικής μεθόδου (βασική αρχή κατασκευής μιας αποδεικτικής επιστήμης).
Ο Ευκλείδης κατέχει μια κρίσιμη θέση στην ιστορία της Λογικής και των Μαθηματικών, καθώς ήταν ο πρώτος που παρήγαγε ένα αυστηρά δομημένο και συνεκτικό σύστημα προτάσεων (θεωρημάτων και πορισμάτων) με βάση ένα σύνολο ορισμών και 5 μόνο αρχικές αναπόδεικτες προτάσεις (αιτήματα). Κατ’ αυτό τον τρόπο περιέλαβε στο σύστημα αυτό και προτάσεις ήδη διατυπωμένες παλαιότερων σημαντικών μαθηματικών, όπως ο Θαλής, ο Πυθαγόρας, ο Θεαίτητος, ο Λεωδάμαντας και ο Εύδοξος.
Τι είναι η αξιωματική μέθοδος;
Η αξιωματική μέθοδος είναι ένας τρόπος για να κατασκευάσουμε μια επιστημονική θεωρία.
Αρχικά εισάγονται, χωρίς ορισμούς, ορισμένες έννοιες που προκύπτουν άμεσα από την εμπειρία μας και λέγονται πρωταρχικές ή αρχικές έννοιες. Οι αρχικές έννοιες για τη Γεωμετρία είναι το σημείο, η ευθεία και το επίπεδο.
- Στη συνέχεια, επιλέγονται κάποιες προτάσεις (ισχυρισμοί) των οποίων η αλήθεια είναι προφανής και λέγονται αξιώματα ή αιτήματα. Κατά τον Αριστοτέλη στο έργο του «Αναλυτικά Ύστερα» τα αιτήματα είναι υποθέσεις τις οποίες δεχόμαστε χωρίς απόδειξη, μολονότι η αλήθειά τους δεν είναι προφανής. Τα αξιώματα αναφέρονται σε ιδιότητες των αρχικών εννοιών. Για παράδειγμα αξιώματα είναι οι προτάσεις: «Από δύο σημεία διέρχεται μία μόνο ευθεία», «Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο του επιπέδου που δεν ανήκει σε αυτή», «Κάθε ευθεία έχει άπειρα σημεία και προεκτείνεται απεριόριστα και προς τις δύο κατευθύνσεις χωρίς διακοπές και κενά».
- Τέλος, έχουμε τα θεωρήματα, τα οποία είναι προτάσεις, η αλήθεια των οποίων προκύπτει με μια σειρά συλλογισμών, που στηρίζονται σε ένα ή περισσότερα αξιώματα ή και σε άλλα γνωστά θεωρήματα. Οι κανόνες στους οποίους βασίζονται οι συλλογισμοί αυτοί είναι το αντικείμενο της Λογικής. Η διαδικασία που μας οδηγεί στην αλήθεια ενός θεωρήματος λέγεται απόδειξη. Επίσης έχουμε και τα πορίσματα τα οποία είναι προτάσεις των οποίων η αλήθεια είναι άμεση συνέπεια ενός θεωρήματος.
Όλες οι επιστήμες που κατασκευάζονται με την αξιωματική μέθοδο λέγονται αποδεικτικές ή παραγωγικές επιστήμες.
Άλλα έργα του Ευκλείδη
Επιπλέον, ο Ευκλείδης έγραψε σωρεία συγγραμμάτων.
Ενδεικτικά:
- «Στοιχεία»: Είναι το γνωστότερο έργο του Ευκλείδη, το οποίο αποτελείται από 13 βιβλία. Αν και γνωστά για τα γεωμετρικά τους αποτελέσματα, τα «Στοιχεία» περιέχουν και τη θεωρία των αριθμών. Θεωρείται η ένωση ανάμεσα στους τέλειους αριθμούς και τους αριθμούς του Μερσέν (γνωστό σαν Θεώρημα Ευκλείδη-Όιλερ), η απειρία των πρώτων αριθμών λήμμα του Ευκλείδη στην παραγοντοποίηση (η οποία οδηγεί στο θεμελιώδες θεώρημα της αριθμητικής, της μοναδικότητας και του Ευκλείδειου αλγορίθμου για την εύρεση του μέγιστου κοινού διαιρέτη δύο αριθμών). Το γεωμετρικό σύστημα που περιγράφεται στα στοιχεία ήταν γνωστό από καιρό απλά ως γεωμετρία, και θεωρήθηκε ότι είναι η μοναδική γεωμετρία. Σήμερα, ωστόσο, το σύστημα αυτό αποκαλείται Ευκλείδεια γεωμετρία για να διακρίνεται από άλλες λεγόμενες μη ευκλείδειες γεωμετρίες που οι μαθηματικοί ανακάλυψαν τον 19ο αιώνα.
- «Οπτικά»: Είναι η αρχαιότερη σωζόμενη ελληνική πραγματεία σχετικά με την προοπτική. Το έργο αυτό περιέχει τις βασικές προτάσεις της γεωμετρικής οπτικής, που είναι βασισμένες στην υπόθεση του Πλάτωνα, σύμφωνα με την οποία η όραση προκαλείται από ακτίνες που προέρχονται από το μάτι.
- «Κατοπτρικά»: Το έργο αυτό ασχολείται με τα φαινόμενα της ανάκλασης του φωτός σε επίπεδα κάτοπτρα. Δεν είναι γνήσιο έργο του Ευκλείδη αν και μπορεί να είναι μεταγενέστερη συλλογή εργασιών του.
- «Φαινόμενα»: Είναι μια πραγματεία κοσμογραφίας, διατυπωμένη με την ίδια αυστηρότητα που είχε εφαρμόσει και στα άλλα έργα του.
- «Δεδομένα»: Το έργο αυτό ασχολείται με μια κατηγορία προτάσεων. Κάθε πρόταση από αυτές αναφέρεται σε ένα σχήμα, του οποίου δίνονται ορισμένα στοιχεία κατά σχήμα, θέση ή μέγεθος.
- «Περί διαιρέσεων»: Το ελληνικό πρωτότυπο κείμενο δεν έχει βρεθεί μέχρι σήμερα. Οι πληροφορίες που έχουμε για το έργο αυτό προέρχονται από την αραβική βιβλιογραφία.
Λίγα λόγια για τον Τζον Νάπιερ
Ο Τζον Νάπιερ (John Napier) ήταν διάσημος μαθηματικός, φυσικός και αστρονόμος με καταγωγή από το Εδιμβούργο της Σκωτίας (1550-1617).
Ως μαθηματικός, ο Νάπιερ, είναι κυρίως γνωστός για την μέθοδο που εισήγαγε σχετικά με την χρήση των λογαρίθμων, καθώς και για την ονομασία τους ως «λογάριθμους». Επίσης, ήταν εκείνος που εφάρμοσε την καθημερινή χρήση του δεκαδικού σημείου στα μαθηματικά και την αριθμητική.
Κατά την ενασχόληση του με τα μαθηματικά, ο Τζον Νάπιερ ασχολήθηκε κυρίως με θέματα υπολογιστικής, όπως τον πολλαπλασιασμό πλεγμάτων, το δεκαδικό σύστημα, την τριγωνομετρία καθώς και τους αστρονομικούς υπολογισμούς. Επιπλέον, εφηύρε την υπολογιστική συσκευή γνωστή ως «κόκκαλα του Νάπιερ» στην οποία χρησιμοποιούνταν ένα σύστημα αρίθμησης με μικρές ράβδους και επισημάνσεις αριθμητικών τιμών πάνω τους, των οποίων οι διακόπτες όταν γυρνούσαν στον κατάλληλο βαθμό ήταν δυνατό να υπολογιστούν τα σωστά γινόμενα και πηλίκα.
Η συνεισφορά του Νάπιερ στα εφαρμοσμένα μαθηματικά έγκειται στις μεθόδους που εισήγαγε, οι οποίες βοήθησαν στην απλοποίηση του αριθμητικού υπολογισμού. Ο Νάπιερ ανέπτυξε επίσης λογαρίθμους. Μάλιστα, υπάρχει μια μαθηματική μονάδα μέτρησης, η οποία σχετίζεται με την περιοχή των τηλεπικοινωνιών, η οποία είναι αφιερωμένη σε εκείνον. Πρόκειται για τον neperio ή neperio.
Ο Νάπιερ είχε επίσης αποκρυφιστικά ενδιαφέροντα, και την εποχή εκείνη είχε και τη φήμη του μάγου. Από νεαρή ηλικία είχε δείξει ιδιαίτερο ενδιαφέρον προς την «Αποκάλυψη του Ιωάννη» και την χρησιμοποίησε προκειμένου να προβλέψει το τέλος του κόσμου στο έργο «A Plaine Discovery of the Whole Revelation of St. John» (1593). Τέλος, αναφέρεται πως ασχολείται με την αλχημεία αλλά και την νεκρομαντεία, ενώ ταξίδευε πάντα μαζί με μια μαύρη αράχνη σε ένα μικρό κουτί.
Το 1617 ο Τζον Νάπιερ προσβλήθηκε από ποδάγρα και απεβίωσε λίγο αργότερα στο κάστρο του Μέρτσιστον όπου είχε γεννηθεί. Τάφηκε στην αυλή του καθεδρικού ναού του Σαιντ Τζάιλς και μετέπειτα μετακινήθηκε στον ναό του Σαιντ Κάθμπερτ στην δυτική πλευρά του Εδιμβούργου.
Θεωρία Παιγνίων: Το «δίλημμα του φυλακισμένου»
Το «δίλημμα του φυλακισμένου» είναι ένα διάσημο νοητικό πείραμα της θεωρίας παιγνίων, το οποίο μπορεί να χρησιμοποιηθεί ως πρότυπο σε πολλές καταστάσεις του πραγματικού κόσμου που αφορούν συμπεριφορές συνεργασίας. Συνοπτικά, το δίλημμα αυτό οδηγεί στο συμπέρασμα πως το βέλτιστο για τον άνθρωπο και το βέλτιστο για την κοινωνία πολύ συχνά δεν συμβαδίζουν.
Το συγκεκριμένο δίλημμα επινοήθηκε και αναλύθηκε από τους Merill Flood και Melvin Dresher, την εποχή του Ψυχρού Πολέμου, στην Καλιφόρνια του 1950, όταν δούλευαν για λογαριασμό της Rand Corporation -του ερευνητικού κέντρου που ήθελε μελέτες στη θεωρία των παιγνίων για να τις χρησιμοποιήσει σε ενδεχόμενο πυρηνικό πόλεμο.
Οι δυο μαθηματικοί ανακάλυψαν ένα απλό μαθηματικό μοντέλο, σε μορφή παιγνίου, που εξετάζει τις στρατηγικές επιλογές λογικά σκεπτόμενων «παικτών» οι οποίοι εμπλέκονται σε ανταγωνιστικές καταστάσεις. Σύμφωνα με αυτό το μοντέλο, οι παίκτες μπορούν είτε να συνεργαστούν μεταξύ τους είτε να προδώσουν ο ένας τον άλλον.
Το «δίλημμα του φυλακισμένου» σχετίζεται με τα κριτήρια εκείνα σύμφωνα με τα οποία δύο οντότητες λαμβάνουν αποφάσεις οδηγούμενοι είτε στο να κερδίσουν σημαντικά οφέλη από τη συνεργασία τους είτε στο να υποστούν την αποτυχία εάν δεν συνεργαστούν. Σύμφωνα ωστόσο μ’ αυτό το μοντέλο και οι δύο πλευρές θεωρούν αδύνατο -ή δαπανηρό- να συντονίσουν τις δραστηριότητες τους για την επίτευξη αυτής της συνεργασίας, καταλήγοντας έτσι να προδίδουν ο ένας τον άλλον αναλογιζόμενοι το ατομικό τους συμφέρον.
Να σημειωθεί πως το συγκεκριμένο νοητικό πείραμα μπορεί να εφαρμοστεί σε διάφορους τομείς της ζωής: από τις επιχειρήσεις, την οικονομία, τα δημοσιονομικά και τις πολιτικές επιστήμες μέχρι τη φιλοσοφία, την ψυχολογία, τη βιολογία και την κοινωνιολογία.
Το σενάριο του «διλήμματος του φυλακισμένου» έχει ως εξής:
Δυο ύποπτοι (Α και Β) έχουν συλληφθεί ως μέλη μιας συμμορίας για ένα έγκλημα και κρατούνται σε χωριστά δωμάτια σε ένα αστυνομικό τμήμα, χωρίς να έχουν δυνατότητα επικοινωνίας μεταξύ τους. Οι Αρχές έχουν έλλειψη επαρκών αποδείξεων για να τους καταδικάσουν με τη βασική κατηγορία. Ταυτόχρονα, ο ανακριτής προσφέρει στους φυλακισμένους μια συμφωνία, έχοντας πει στον καθένα τα ακόλουθα:
- Εάν ομολογήσεις και συμφωνήσεις να καταθέσεις εναντίον του άλλου υπόπτου, ότι διέπραξε έγκλημα, οι κατηγορίες εναντίον σου θα αποσυρθούν και θα αφεθείς ελεύθερος ατιμώρητος.
- Εάν δεν ομολογήσεις και το κάνει ο άλλος ύποπτος, θα καταδικαστείς με τη μέγιστη ποινή των 3 ετών.
- Εάν ομολογήσετε και οι δυο, θα καταδικαστείτε με 2 χρόνια κάθειρξη έκαστος.
- Εάν κανείς από τους δυο δεν ομολογήσει και οι δυο θα κατηγορηθείτε για πταίσμα και θα καταδικαστείτε με 1 χρόνο φυλακή.
Η ουσία του διλήμματος είναι τι θα κάνουν οι ύποπτοι και η θεωρία παιγνίων διερωτάται ποια είναι η αναμενόμενη ορθολογικά «βέλτιστη» στάση του καθενός από τους φυλακισμένους.
Ο Β είτε θα συνεργαστεί (μένει σιωπηλός), είτε θα αποστατήσει (ομολογεί). Εάν ο Β μείνει σιωπηλός, ο Α σκέφτεται πως πρέπει να ομολογήσει, γιατί το να αφεθεί ελεύθερος, είναι καλύτερα από το να πάει 1 χρόνο φυλακή. Αν ο Β ομολογήσει, ο Α σκέφτεται πως πρέπει επίσης να ομολογήσει, γιατί το να πάει φυλακή 2 χρόνια είναι καλύτερο από το να πάει 3. Έτσι, σε κάθε περίπτωση, ο Α σκέφτεται πως τον συμφέρει να ομολογήσει. Αντίστοιχα σκέφτεται και ο Β.
Ομολογουμένως, η καλύτερη στρατηγική είναι να ομολογήσεις, αδιαφορώντας για το τι θα κάνει ο άλλος ύποπτος, μας λέει η θεωρία των παιγνίων.
Ωστόσο, παρ’ όλο που και οι δυο «λογικά» σκεπτόμενοι το συμφέρον τους αποφασίζουν να ομολογήσουν εναντίον του συνενόχου τους, ο καθένας βρίσκεται σε χειρότερη θέση, από το να έμεναν και οι δυο σιωπηλοί. Και οι δυο ήλπιζαν πως ο άλλος δεν θα μιλούσε και θα αφήνονταν ελεύθεροι. Ωστόσο ο εγωισμός τους δεν έφερε το καλύτερο αποτέλεσμα και για τους δυο, δηλαδή να μην προδώσει ο ένας τον άλλον και να κάνουν μόνο 1 χρόνο φυλακή.
Τα αποτελέσματα είναι χειρότερα από ότι αν ο καθένας διάλεγε να ελαχιστοποιήσει το διάστημα της ποινής του συνεργού του, με το κόστος να ξοδέψει ο ίδιος περισσότερο χρόνο στη φυλακή.
Αν και η θεωρία παιγνίων υποστηρίζει πως οι απόλυτα «λογικοί» θα προδώσουν τον άλλον, στην ουσία διαπιστώνουμε πως ο εγωισμός και η ιδιοτέλεια… κοστίζουν.
Αλλά γιατί δυο απόλυτα λογικοί άνθρωποι δεν πέτυχαν το βέλτιστο και για τους δυο αποτέλεσμα και δεν κατάφεραν να κρατήσουν τη σιωπή τους και να πάνε φυλακή με ποινή μόνο ενός έτους;
Αν συγκρίνουμε τις επιλογές που έχει ο καθένας, θα διαπιστώσουμε πως για κάθε επιλογή του να μιλήσει ή να μη μιλήσει, η επιλογή με το καλύτερο αποτέλεσμα είναι να καρφώσει τον συνένοχο. Με δεδομένη κάθε επιλογή του αντιπάλου, το αποτέλεσμα του ανταγωνισμού επικρατεί έναντι του αποτελέσματος της συνεργασίας.
Το παράδειγμα δείχνει πως το «κοινό συμφέρον» δεν είναι πάντα η επιλογή απόλυτα λογικά σκεπτόμενων ανθρώπων και πως συχνά απόλυτα «λογικές» επιλογές μπορεί να οδηγήσουν σε ζημία όλους τους εμπλεκόμενους.
YouTube Link: https://youtu.be/17o8CIeXV2Y
Μπλεζ Πασκάλ: Ένας χαρισματικός μαθηματικός και φιλόσοφος
Ο Μπλεζ Πασκάλ γεννήθηκε στις 19 Ιουνίου 1623 στο Κλερμόν-Φεράν και απεβίωσε στο Παρίσι στις 19 Αυγούστου 1662. Από μικρός ήταν παιδί-θαύμα, ενώ μεγαλώνοντας αναδείχθηκε ως σπουδαίος μαθηματικός, φυσικός, συγγραφέας, αλλά και φιλόσοφος. Αξίζει να αναφέρουμε πως αν και ο Πασκάλ ήταν ιδιαίτερα έξυπνος, δεν απέκτησε ποτέ ακαδημαϊκή καριέρα σε κάποιο πανεπιστήμιο.
Από μικρή ηλικία όμως καταπιανόταν με διάφορες εφευρέσεις-ανακαλύψεις. Ήταν μόλις 16 ετών, όταν ανέπτυξε σε μια πραγματεία περί κωνικών τομών το θεώρημα που φέρει το όνομά του. Στη συνέχεια, από το 1641 και για περίπου 3 χρόνια, εργάστηκε σκληρά για την κατασκευή μιας αριθμομηχανής, η οποία μπορούσε να κάνει πρόσθεση και αφαίρεση, γνωστή ως «Πασκαλίνα». Ωστόσο, παρά την έντονη ενασχόληση του μ’ αυτό ο Μπλεζ Πασκάλ δεν πέτυχε ως επιχειρηματίας αριθμομηχανών, εφόσον η μηχανή του δεν έκανε μεγάλες πωλήσεις και, τελικά, σταμάτησε να παράγεται.
Λίγο αργότερα, το 1647 ανακάλυψε την «Αρχή του Πασκάλ» και τη χρήση του βαρομέτρου για τη μέτρηση του υψομέτρου. Μάλιστα, με την εργασία του «Traité du triangle arithmétique» (1654), ο ίδιος έθεσε τις βάσεις για την Συνδυαστική και το Λογισμό των Πιθανοτήτων.
Επιπλέον, αξίζει να γνωρίζουμε πως μια από τις πιο γνωστές μαθηματικές μελέτες του Γάλλου αυτού μαθηματικού είναι αυτό που ονομάζουμε «τρίγωνο του Πασκάλ», ή πιο απλά «αριθμητικό τρίγωνο».
Στα τελευταία χρόνια της ζωής του, αποτραβήχτηκε κάπως από τα μαθηματικά και εστίασε περισσότερο την προσοχή του στη συγγραφή θρησκευτικών συγγραμμάτων. Επιπλέον, το 1654 είχε την εμπειρία ενός μυστικιστικού οράματος, οπότε αποσύρθηκε στο μοναστήρι Port Royal και αφοσιώθηκε, παράλληλα με τις μαθηματικές εργασίες του, σε θεολογικές και φιλοσοφικές μελέτες. Ο μεγάλος αυτός φιλόσοφος κατέληξε, έπειτα από επιδείνωση των προβλημάτων υγείας που αντιμετώπιζε για κάμποσα χρόνια, στο Παρίσι το 1662, σε ηλικία μόλις 39 ετών, ενώ προς τιμήν του δόθηκε το όνομά του στη μονάδα μέτρησης της πίεσης στο SI (1 Pa).