Home » Articles posted by e-diakrisi (Page 4)
Author Archives: e-diakrisi
Η Εξίσωση Σρέντινγκερ: Το Θεμέλιο της Κβαντικής Μηχανικής
Η εξίσωση Σρέντινγκερ αποτελεί έναν από τους πυλώνες της κβαντικής μηχανικής, του πεδίου της φυσικής που μελετά τη συμπεριφορά των σωμάτων σε μικρές κλίμακες, όπως ατομικά και υποατομικά επίπεδα. Η εξίσωση αυτή περιγράφει τον τρόπο με τον οποίο η κβαντική κατάσταση ενός φυσικού συστήματος εξελίσσεται χρονικά και πώς επηρεάζεται από εξωτερικές δυνάμεις.
Η Διατήρηση της Ενέργειας και το Παράδοξο των Κυμάτων
Τον 20ό αιώνα, οι φυσικοί αντιλήφθηκαν ότι οι κλασικές αρχές της φυσικής, όπως οι νόμοι της κινητικής του Νεύτωνα και οι εξισώσεις της ηλεκτροδυναμικής του Μαξγουέλ, απέτυχαν να περιγράψουν ορισμένα φαινόμενα σε πολύ μικρές κλίμακες, όπως αυτά που συμβαίνουν στον κόσμο των ατόμων και των υποατομικών σωματιδίων. Το γεγονός ότι τα σωματίδια σε αυτό το επίπεδο φαίνονταν να συμπεριφέρονται ως κύματα αντί για σωματίδια προκάλεσε μεγάλη αναταραχή.
Με την προσπάθειά τους να αναλύσουν αυτό το φαινόμενο, οι φυσικοί κατέληξαν στην ανάγκη ενός νέου μαθηματικού πλαισίου που θα μπορούσε να αποδεικνύει τις παρατηρήσεις τους. Και έτσι γεννήθηκε η κβαντική μηχανική.
Η Εξίσωση Σρέντινγκερ
Το 1925, ο φυσικός Έργκ Σρέντινγκερ διατύπωσε την εξίσωση που κρύβεται πίσω από αυτό το νέο πλαίσιο. Η εξίσωση Σρέντινγκερ είναι μια περιορισμένη χρονοεξαρτώμενη εξίσωση κύματος, που περιγράφει πώς μια κβαντική κατάσταση εξελίσσεται χρονικά.
Η εξίσωση Σρέντινγκερ δίνει τη δυνατότητα να προβλέψουμε την πιθανότητα μιας σωματιδιακής θέσης, ταχύτητας ή ενέργειας κατά τη διάρκεια ενός χρονικού διαστήματος. Είναι αυτή η πιθανοκρατική φύση που διακρίνει την κβαντική μηχανική από την κλασική φυσική και που προκαλεί πολλά από τα παράξενα φαινόμενα που παρατηρούμε σε αυτό το επίπεδο.
Εφαρμογές και Σημασία
Η εξίσωση Σρέντινγκερ είναι βασικό εργαλείο για την πρόβλεψη της συμπεριφοράς των κβαντικών σωματιδίων, όπως ηλεκτρόνια και φωτόνια. Είναι κρίσιμη για την ανάπτυξη κβαντικών υπολογιστών, την κβαντική χημεία και τις τεχνολογίες φωτονικής.
Συνοψίζοντας, η εξίσωση Σρέντινγκερ αποτελεί το θεμέλιο της κβαντικής μηχανικής και είναι απαραίτητη για την κατανόηση των συμπεριφορών και των φαινομένων σε πολύ μικρές κλίμακες. Με τη βοήθειά της, η ανθρώπινη γνώση έχει επεκταθεί σε νέους και απροσδιόριστους κόσμους που παραμένουν εντυπωσιακοί και μυστηριώδεις.
Η υπόθεση των Birch και Swinnerton-Dyer
Η υπόθεση των Birch και Swinnerton-Dyer είναι ένα από τα πιο σημαντικά ανοιχτά προβλήματα στη θεωρία των αριθμητικών ελλείψεων και σχέσεων μεταξύ αριθμητικής και αλγεβρικής γεωμετρίας. Αυτή η υπόθεση προέκυψε από το έργο των μαθηματικών Bryan Birch και Peter Swinnerton-Dyer στη δεκαετία του 1960.
Συγκεκριμένα, η υπόθεση αφορά τις ελλείψεις της μορφής y^2 = x^3 + ax + b, όπου a και b είναι ακέραιοι αριθμοί και οι λύσεις (x, y) είναι ακέραιοι αριθμοί επίσης. Η υπόθεση των Birch και Swinnerton-Dyer προβλέπει ότι υπάρχει μια στενή σχέση μεταξύ της ανάλυσης των ελλείψεων αυτών και της θεωρίας των αβελιανών πολλαπλοτήτων, μιας κλάσης αλγεβρικών γεωμετρικών αντικειμένων.
Η υπόθεση εκφράζει ότι η έλλειψη παρουσιάζει μια ιδιαίτερη δομή, γνωστή ως αναλυτική περίοδος, η οποία είναι συνδεδεμένη με την τάξη της αβελιανής πολλαπλότητας. Ειδικότερα, αν η αναλυτική περίοδος είναι μη μηδενική, τότε η έλλειψη έχει άπειρα πολλαπλά σημεία, ενώ αν είναι μηδενική, τότε η έλλειψη έχει μόνο έναν πεπερασμένο αριθμό λύσεων. Η υπόθεση των Birch και Swinnerton-Dyer προτείνει ότι η πολυπλοκότητα των ελλείψεων συνδέεται άμεσα με την πολυπλοκότητα της αβελιανής πολλαπλότητας που σχετίζεται με αυτές.
Παρόλο που η υπόθεση των Birch και Swinnerton-Dyer έχει εξεταστεί εκτενώς και έχουν προταθεί πολλές προσεγγίσεις και αποδείξεις για συγκεκριμένες περιπτώσεις, ακόμα δεν έχει βρεθεί γενική απόδειξη. Αυτό το καθιστά ένα ανοιχτό μαθηματικό πρόβλημα που συνεχίζει να προβληματίζει τους μαθηματικούς και να παραμένει ένα από τα μεγάλα μυστήρια της αριθμητικής θεωρίας.
Η υπόθεση των Birch και Swinnerton-Dyer ανήκει σε μια ειδική λίστα ανοιχτών προβλημάτων στα μαθηματικά γνωστή ως τα “Millennium Problems” που παρουσιάστηκαν από το Ινστιτούτο Clay. Για την επίλυση κάθε προβλήματος σε αυτήν τη λίστα προσφέρεται χρηματικό έπαθλο 1 εκατομμύριο δολάρια.
Χέρμαν φον Χέλμχολτς: Ένας διακεκριμένος επιστήμονας με πλούσια επιστημονική συμβολή
Ο Χέρμαν φον Χέλμχολτς (1821-1894) γεννήθηκε στο Potsdam της Γερμανίας. Ήταν ένας Γερμανός φυσικός και επιστήμονας με ευρεία γνώση σε πολλά επιστημονικά πεδία. Η συνεισφορά του Χέλμχολτς στην επιστήμη κάλυπτε ένα ευρύ φάσμα θεμάτων, συμπεριλαμβανομένης της οπτικής, της ακουστικής, της μηχανικής, της υδροδυναμικής, του ηλεκτρομαγνητισμού, των μαθηματικών και της ιατρικής.
Είναι ευρέως γνωστός ως συνεφευρέτης (μαζί με τον Τζουλ και τον Τζούλιους Μέγιερ) του νόμου της διατήρησης της ενέργειας. Επέκτεινε επίσης τη θεωρία του Τόμας Γιάνγκ για το χρώμα της όρασης, γνωστή σήμερα ως η θεωρία του ζευγαριού-Χέλμχολτς. Αυτή η θεωρία αναφέρεται στην ανάλυση των χρωμάτων του οπτικού φάσματος από το ανθρώπινο μάτι.
Ο Χέλμχολτς διατύπωσε επίσης τη θεωρία της απήχησης της ακοής, η οποία αναφέρεται στη χρήση των αντηχείων (που σήμερα είναι γνωστά ως αντηχεία Χέλμχολτς) για την ανάλυση πολύπλοκων ήχων. Επιπλέον, ο ίδιος συνεισέφερε σημαντικά στη θεωρία της μουσικής, καθώς μελέτησε την φύση των μουσικών ήχων και ανέπτυξε μαθηματικά μοντέλα για την κατανόηση της μουσικής αρμονίας και της αντίληψης των μελωδιών.
Επίσης, ο Χέρμαν φον Χέλμχολτς κατασκεύασε μια γενικευμένη μορφή της ηλεκτρομαγνητικής θεωρίας, γνωστή ως εξίσωση του ηλεκτρομαγνητικού κύματος. Αυτή η εξίσωση, που αποδίδεται στο όνομά του, περιέγραψε τη συμπεριφορά των ηλεκτρομαγνητικών κυμάτων και είχε σημαντική επίδραση στην ανάπτυξη της ηλεκτρομαγνητικής θεωρίας γενικότερα.
Τέλος, η ευρεία γνώση του Χέρμαν φον Χέλμχολτς και η εφαρμογή των μαθηματικών στις επιστημονικές του μελέτες τον καθιστούν έναν από τους πιο σημαντικούς επιστήμονες του 19ου αιώνα.
Λίγα λόγια για τη ζωή του Βρετανού φυσικού Τζον Ντάγκλας Κόκροφτ
Ο Τζον Ντάγκλας Κόκροφτ (John Douglas Cockcroft) ήταν Βρετανός φυσικός, ο οποίος είναι περισσότερο γνωστός για το πρωτοποριακό έργο του στον τομέα της πυρηνικής φυσικής.
Ο Κόκροφτ γεννήθηκε στις 27 Μαΐου 1897 στο Τοντμόρντεν, μια μικρή πόλη στο Δυτικό Γιορκσάιρ της Αγγλίας. Αξίζει να αναφέρουμε πως ο Κόκροφτ σπούδασε φυσική στο Πανεπιστήμιο του Μάντσεστερ, όπου έλαβε το πτυχίο του το 1924 και στη συνέχεια, το διδακτορικό του το 1928.
Τη δεκαετία του 1930, ο Κόκροφτ εργάστηκε με τον Έρνεστ Τόμας Σάιντον Γουόλτον στο Εργαστήριο Κάβεντις του Πανεπιστημίου του Κέιμπριτζ, όπου διεξήγαγαν πρωτοποριακά πειράματα. Σε αυτά τους τα πειράματα οι δύο επιστήμονες χρησιμοποίησαν έναν επιταχυντή σωματιδίων προκειμένου να διασπάσουν τους πυρήνες των ατόμων. Το έργο αυτό οδήγησε στην ανάπτυξη του πρώτου πυρηνικού αντιδραστήρα, καθώς και του πρώτου πυρηνικού όπλου.
Κατά τη διάρκεια του Β’ Παγκοσμίου Πολέμου, ο Κόκροφτ συμμετείχε στην ανάπτυξη του ραντάρ και διετέλεσε διευθυντής του Atomic Energy Research Establishment στο Χάργουελ του Οξφορντσάιρ από το 1946 έως το 1954. Εν συνεχεία, το 1951, ο Τζον Ντάγκλας Κόκροφτ χρίστηκε ιππότης για τη συμβολή του στην επιστήμη.
Αφού αποσύρθηκε από τη θέση του στο Χάργουελ, ο Κόκροφτ υπηρέτησε ως διευθυντής του Κολλεγίου Τσόρτσιλ στο Πανεπιστήμιο του Κέιμπριτζ από το 1959 έως το 1967. Διετέλεσε επίσης πρόεδρος του Ινστιτούτου Φυσικής από το 1954 έως το 1956 και τιμήθηκε με το Τάγμα της Αξίας το 1967.
Ο Κόκροφτ πέθανε στις 18 Σεπτεμβρίου 1967, σε ηλικία 70 ετών. Η συμβολή του στον τομέα της πυρηνικής φυσικής είχε σημαντικό αντίκτυπο στην ανάπτυξη της σύγχρονης τεχνολογίας και συνεχίζει να επηρεάζει, μέχρι και σήμερα την επιστημονική έρευνα.
Λίγα λόγια για τις εξισώσεις Navier-Stokes
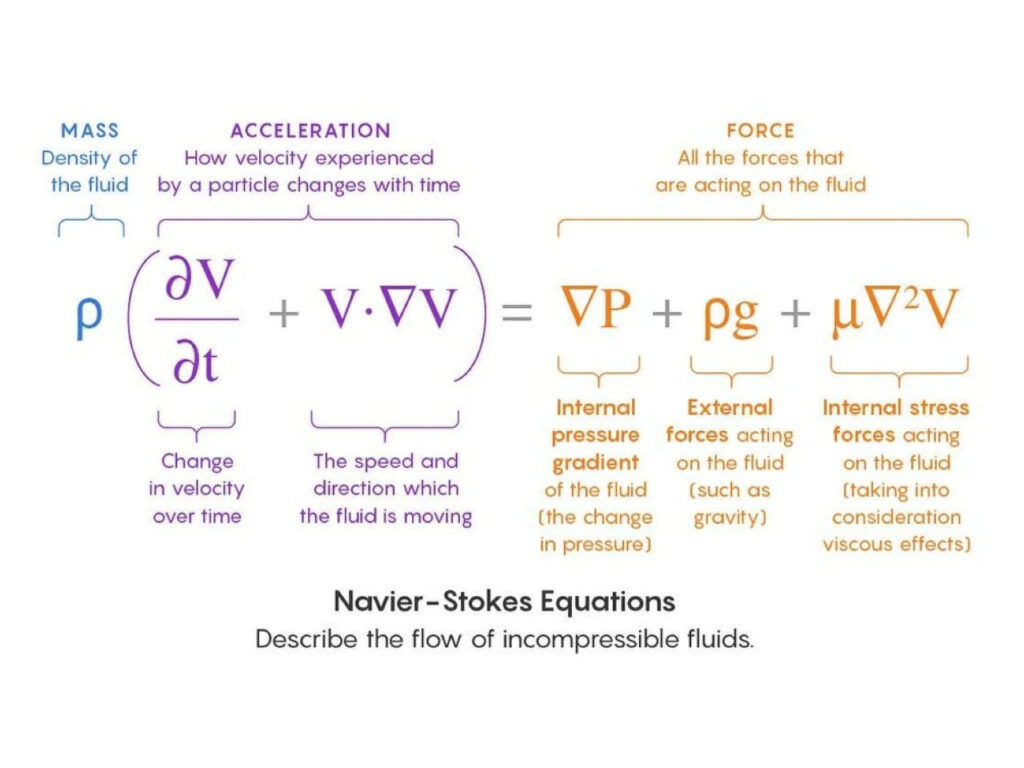
Οι εξισώσεις Navier-Stokes είναι ένα σύνολο μερικών διαφορικών εξισώσεων που περιγράφουν την κίνηση των ρευστών. Οι συγκεκριμένες εξισώσεις πήραν το όνομά τους από τον Γάλλο μαθηματικό και φυσικό Κλοντ-Λουί Ναβιέ (Claude-Louis Navier) και τον Ιρλανδό μαθηματικό και φυσικό George Gabriel Stokes (Τζορτζ Γκάμπριελ Στόουκς). Αξίζει να αναφέρουμε πως αυτές οι εξισώσεις περιγράφουν τη διατήρηση της μάζας και της ορμής σε ένα ρευστό, λαμβάνοντας υπόψη τις επιδράσεις του ιξώδους και των εξωτερικών δυνάμεων. Μπορούν να γραφούν σε διανυσματική μορφή ως εξής:
∂ρ/∂t + ∇-(ρv) = 0
ρ (∂v/∂t + v-∇v) = -∇p + ∇-τ + f
Όπου:
● ρ είναι η πυκνότητα του ρευστού,
● v είναι το διάνυσμα ταχύτητας του ρευστού,
● p είναι η πίεση,
● τ είναι ο τανυστής ιξώδους τάσης,
● f είναι κάθε εξωτερική δύναμη που ασκείται στο ρευστό, όπως η βαρύτητα¨.
Η πρώτη εξίσωση είναι η εξίσωση συνέχειας, η οποία δηλώνει ότι ο ρυθμός μεταβολής της πυκνότητας σε οποιοδήποτε στοιχείο του ρευστού είναι ίσος με την αρνητική απόκλιση της ταχύτητας του ρευστού. Η δεύτερη εξίσωση είναι η εξίσωση ορμής, η οποία δηλώνει ότι ο ρυθμός μεταβολής της ορμής σε οποιοδήποτε στοιχείο του ρευστού είναι ίσος με το άθροισμα των δυνάμεων που ασκούνται στο στοιχείο αυτό.
Οι εξισώσεις Navier-Stokes είναι εξαιρετικά μη γραμμικές και δύσκολα επιλύονται αναλυτικά, ακόμη και για απλές γεωμετρίες και οριακές συνθήκες. Μάλιστα, έχουν σημαντικές εφαρμογές σε πολλούς τομείς, όπως η δυναμική των ρευστών, η αεροδυναμική και η πρόβλεψη του καιρού.
Όσα πρέπει να γνωρίζεις για τον Γιόχαν Καρλ Φρίντριχ Γκάους
Ο Γιόχαν Καρλ Φρίντριχ Γκάους, ο οποίος έμεινε γνωστός ως ο «Πρίγκιπας των Μαθηματικών», ήταν ένα παιδί-θαύμα, καθώς έκανε την πρώτη του σημαντική ανακάλυψη στην εφηβεία του. Έγραψε το περίφημο “Disquisitiones Arithmeticae”, το σπουδαιότερο έργο του, σε ηλικία μόλις 21 ετών.
Οι περισσότεροι γνωρίζουν τον Γιόχαν Καρλ Φρίντριχ Γκάους για την εξαιρετική ψυχική του ικανότητα. Αναφέρεται μάλιστα, ότι είχε προσθέσει τους αριθμούς από το 1 έως το 100, μέσα σε μόλις λίγα δευτερόλεπτα, ενώ βρισκόταν ακόμη στο δημοτικό σχολείο, με τη βοήθεια ενός έξυπνου τεχνάσματος
Ο Γερμανός μαθηματικός Γιόχαν Καρλ Φρίντριχ Γκάους συνεισέφερε σε πολλά ερευνητικά πεδία της επιστήμης του, όπως η Θεωρία Αριθμών, η Στατιστική, η Μαθηματική Ανάλυση, η Διαφορική Γεωμετρία, αλλά και συναφών επιστημών, όπως η Γεωδαισία, η Αστρονομία και η Φυσική. Ο ίδιος θέλησε να αποδείξει το θεμελιώδες θεώρημα της Άλγεβρας, και εισήγαγε την “Gaussian” βαρυτική σταθερά στη φυσική, καθώς και πολλά άλλα πριν καν γίνει 24 ετών!
Τέλος, ο Γιόχαν Καρλ Φρίντριχ Γκάους συνέχισε το σπουδαίο έργο του μέχρι τον θάνατό του, σε ηλικία 77 χρόνων, συμβάλλοντας δυναμικά στην πρόοδο και την εξέλιξη της επιστήμης του.
Ο δεύτερος θερμοδυναμικός νόμος
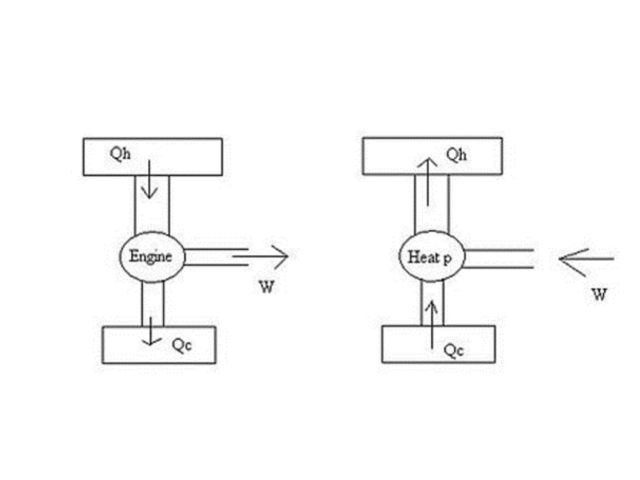
Ο δεύτερος θερμοδυναμικός νόμος είναι ένας από τους σημαντικότερους νόμους της θερμοδυναμικής. Αξίζει να αναφέρουμε πως υπάρχουν δύο (2) ισοδύναμες βασικές διατυπώσεις του νόμου αυτού:
1.Κάθε θερμική μηχανή έχει απώλειες ενέργειας.
2.Για τη λειτουργία μιας ψυκτικής μηχανής απαιτείται καταβολή ενέργειας.
Εξετάζοντας τον νόμο με βάση την εντροπία με κάθε μεταβολή που γίνεται στο σύστημα η συνολική εντροπία μεγαλώνει και μόνο στην ιδανική περίπτωση των αντιστρεπτών μεταβολών μένει σταθερή. Ουσιαστικά, ο νόμος αυτός μας δείχνει ότι η θερμότητα δεν μπορεί να περάσει αυθόρμητα από ένα σώμα σ’ ένα άλλο, θερμότερο από το αρχικό.
Τέλος, να αναφέρουμε πως ο 2ος θερμοδυναμικός νόμος πρωτοδιατυπώθηκε το 1865 από τον Γερμανό φυσικό Ρούντολφ Κλαούζιους (Rudolf Julius Emmanuel Clausius, 2 Ιανουαρίου 1822 – 24 Αυγούστου 1888), ο οποίος θεωρείται ο θεμελιωτής της θερμοδυναμικής.Η διατύπωση του 2ου θερμοδυναμικού νόμου οδήγησε σε τεχνολογίες όπως οι κινητήρες εσωτερικής καύσης, η κρυογενετική και οι γεννήτριες.
Περιγραφή του Φαινομένου Κόμπτον
O Κόμπτον και οι συνεργάτες του απέδειξαν ήδη από το 1922 πως η κλασική φυσική δεν μπορούσε να εξηγήσει τη σκέδαση των ακτίνων Χ από τα ηλεκτρόνια. Σύμφωνα με τη συμβατική εξήγηση, το ηλεκτρόνιο ταλαντώνεται όταν οι ακτίνες Χ το χτυπούν. Αμέσως μετά, το ηλεκτρόνιο αποκτά ταχύτητα και αρχίζει να απελευθερώνει ηλεκτρομαγνητική ενέργεια. Ανάλογα με το πόσο καιρό εκτίθεται το ηλεκτρόνιο στην ακτινοβολία και πόσο έντονη είναι αυτή, η ακτινοβολία αυτή θα έχει μια συχνότητα. Ωστόσο, το πείραμα απέδειξε ότι η συχνότητα της σκεδαζόμενης ακτινοβολίας εξαρτάται αποκλειστικά από τη γωνία σκέδασης. Ως εκ τούτου, η συμβατική εξήγηση δεν ήταν σε θέση να εξηγήσει επαρκώς το συγκεκριμένο φαινόμενο.
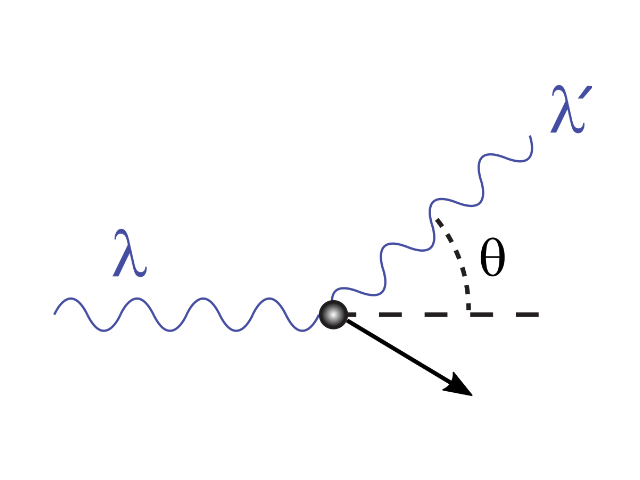
Μετρώντας τα μήκη κύματος και την ένταση των σκεδαζόμενων δεσμών και εκτελώντας το πείραμα σε διάφορες γωνίες σκέδασης, ο Κόμπτον μπόρεσε να εντοπίσει δύο κορυφές στη γραφική παράσταση της έντασης σε σχέση με το μήκος κύματος.
Συγκεκριμένα, η πρώτη κορυφή αντιστοιχούσε σε μήκος κύματος λ, που ήταν το μήκος κύματος της αρχικής δέσμης. Η δεύτερη κορυφή αντιστοιχούσε σε μήκος κύματος λ’, του οποίου η σχέση με τη γωνία σκέδασης φαινόταν από τον εξής τύπο:
Να σημειωθεί πως όπου h η σταθερά δράσεως του Πλάνκ, me η μάζα ηρεμίας του ηλεκτρονίου και c η ταχύτητα του φωτός.
Για τη θεωρητική του εξαγωγή διατυπώθηκαν οι ακόλουθες υποθέσεις:
- Η προσπίπτουσα ηλεκτρομαγνητική ακτινοβολία αποτελείται από φωτόνια με ενέργεια που δίνεται από τον τύπο του Πλανκ (E=hν)
- Τα φωτόνια, όντας σωματίδια, σκεδάζονται από ελαφρώς δέσμια ατομικά ηλεκτρόνια
- Τα ηλεκτρόνια κινούνται με σχετικιστικές ταχύτητες
- Η ενέργεια και η ορμή πριν και μετά την σκέδαση είναι διατηρούμενες ποσότητες
Συνεπώς, ο φαινόμενο αυτό αποτελεί μια από τις πρώτες επιτυχίες της κβαντικής θεωρίας εξαιτίας των παραπάνω παραγόντων.
Η ανακάλυψη της ηλεκτρικής μπαταρίας
Ο Αλεσάντρο Βόλτα, το πλήρες όνομα του οποίου είναι Conte Alessandro Giuseppe Antonio Anastasio Volta, ήταν Ιταλός επιστήμονας. Γεννήθηκε στο Κόμο της Λομβαρδίας στις 18 Φεβρουαρίου 1745 και πέθανε εκεί στις 5 Μαρτίου 1827. Η ανακάλυψη της ηλεκτρικής μπαταρίας του λειτούργησε ως η πρώτη πηγή συνεχούς ρεύματος.
Λίγα λόγια για τον Βόλτα και την ανακάλυψή του
Το 1774, ο Αλεσάντρο Βόλτα διορίστηκε καθηγητής φυσικής στη Βασιλική Σχολή του Κόμο. Η αγάπη του για τον ηλεκτρισμό τον ενέπνευσε να βελτιώσει τον ηλεκτροφόρο, μια μηχανή που παρήγαγε στατικό ηλεκτρισμό, το 1775. Λίγο αργότερα το 1776, ο Βόλτα ανακάλυψε και καθάρισε το αέριο μεθάνιο. Τρία χρόνια αργότερα του ανατέθηκε η έδρα της φυσικής στο Πανεπιστήμιο της Παβίας.
Ο Λουίτζι Γκαλβάνι, φίλος του Βόλτα, ανέφερε το 1791 ότι παράγεται ηλεκτρικό ρεύμα όταν δύο διαφορετικά μέταλλα έρχονται σε επαφή με τους μύες των ποδιών ενός γδαρμένου βατράχου, με αποτέλεσμα το άκρο να συσπάται. Ο Γκαλβάνι θεώρησε ότι αυτό ήταν η ανακάλυψη ενός νέου τύπου ηλεκτρισμού, τον οποίο ονόμασε «ζωικό ηλεκτρισμό», σε ζωντανούς ιστούς.
Ωστόσο, ο Βόλτα πίστευε πως ο βάτραχος απλώς διηύθυνε αυτό που ονόμασε «μεταλλικό ηλεκτρισμό», ένα ρεύμα που ρέει δηλαδή μεταξύ των δύο μετάλλων. Το 1792 ο Βόλτα άρχισε να ερευνά αποκλειστικά με μέταλλα. Μάλιστα, κατά τη διάρκεια της μελέτης και των πειραμάτων του, ο Ιταλός επιστήμονας τοποθετούσε δίσκους από διάφορα μέταλλα στη γλώσσα του για να αισθάνεται το ασθενές ηλεκτρικό ρεύμα που ρέει μεταξύ τους.
Έτσι, ο Αλεσάντρο Βόλτα ανακάλυψε ότι δεν απαιτείται ζωικός ιστός για την παραγωγή ρεύματος. Αξίζει να σημειωθεί πως όταν ο Βόλτα ανακοίνωσε την πρώτη ηλεκτρική μπαταρία το 1800, έβαλε τέλος στη σφοδρή διαμάχη μεταξύ των υποστηρικτών του ζωικού και του μεταλλικού ηλεκτρισμού.
Η μπαταρία του Βόλτα, που συχνά αναφέρεται ως βολταϊκή στήλη (ή αλλιώς βολταϊκός σωρός), αποτελούνταν από εναλλασσόμενους δίσκους ψευδαργύρου και αργύρου (ή χαλκού και κασσίτερου), οι οποίοι χωρίζονταν μεταξύ τους με φύλλα χαρτιού ή υφάσματος βουτηγμένα σε αλατόνερο ή υδροξείδιο του νατρίου.
Το δημιούργημά του πυροδότησε ένα νέο κύμα ηλεκτρικών πειραμάτων, καθώς ήταν μια εύχρηστη, αξιόπιστη πηγή ηλεκτρικού ρεύματος που δεν απαιτούσε επαναφόρτιση. Μέσα σε έξι εβδομάδες από την ανακοίνωση του Βόλτα, οι Άγγλοι ερευνητές Γουίλιαμ Νίκολσον και Άντονι Καρλίσλι χρησιμοποίησαν έναν σωρό Βόλτα για να μετατρέψουν το νερό σε υδρογόνο και οξυγόνο. Αυτή η ανακάλυψη της ηλεκτρόλυσης – η διαδικασία με την οποία ένα ηλεκτρικό ρεύμα προκαλεί μια χημική αντίδραση – οδήγησε στην ανάπτυξη του τομέα της ηλεκτροχημείας.
Να αναφέρουμε επίσης πως ο Ναπολέων έκανε τον Βόλτα κόμη και γερουσιαστή του βασιλείου της Λομβαρδίας, καθώς ο Ιταλός επιστήμονας παρουσίασε μπροστά του την παραγωγή ηλεκτρικού ρεύματος από την μπαταρία του το 1801 στο Παρίσι. Εν συνεχεία, το 1815, διορίστηκε διευθυντής της φιλοσοφικής σχολής του Πανεπιστημίου της Πάντοβα από τον Αυστριακό αυτοκράτορα Φραγκίσκο Α. Τέλος, το 1881, ο Βόλτα συνέβαλε στην έμπνευση για τη δημιουργία του βολτ – μιας μέτρησης της ηλεκτροκινητικής δύναμης που τροφοδοτεί τον ηλεκτρισμό.